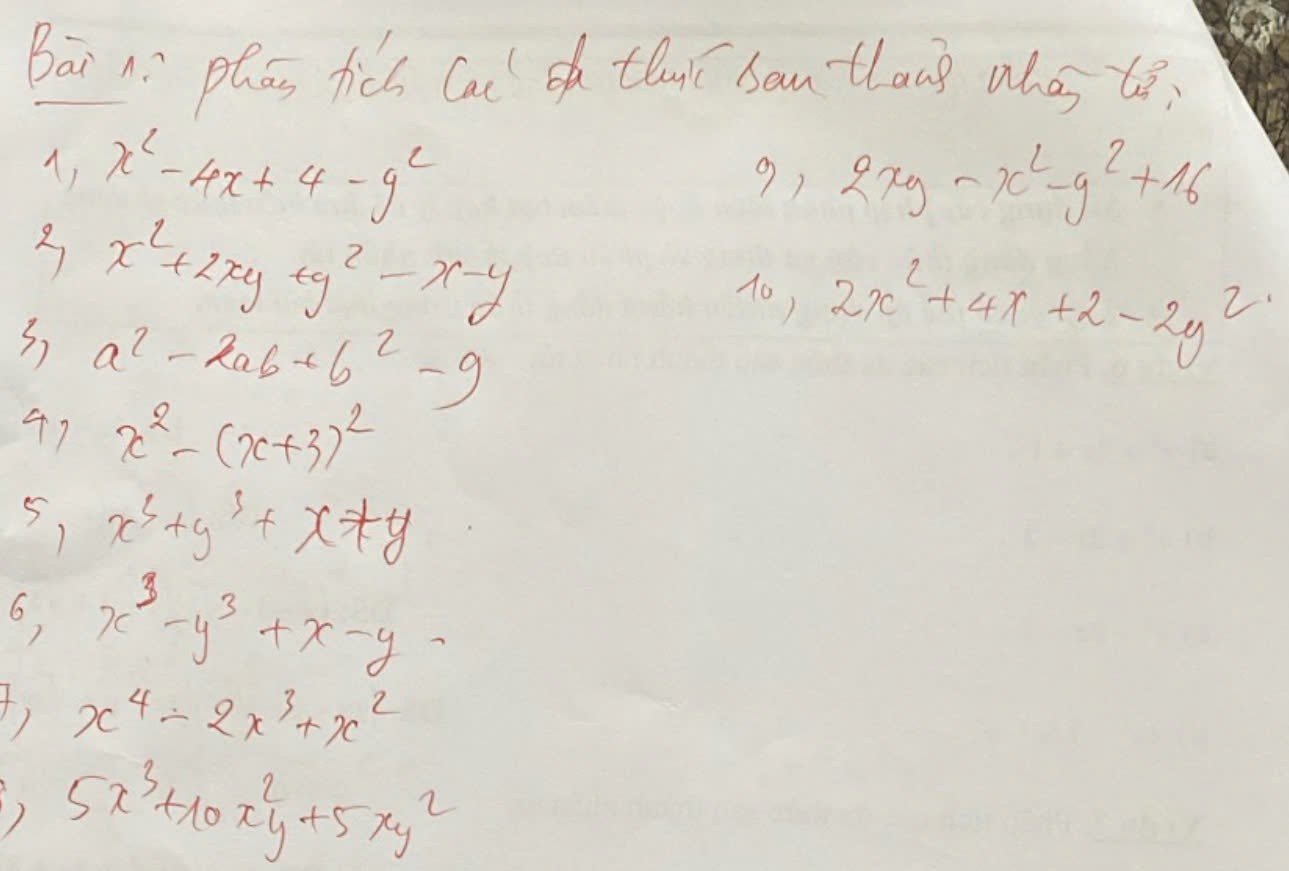1: \(x^2-4x+4-y^2\)
\(=\left(x-2\right)^2-y^2\)
=(x-2-y)(x-2+y)
2: \(x^2+2xy+y^2-x-y\)
\(=\left(x+y\right)^2-\left(x+y\right)\)
=(x+y)(x+y-1)
3: \(a^2-2ab+b^2-9\)
\(=\left(a-b\right)^2-3^2\)
=(a-b-3)(a-b+3)
4: \(x^2-\left(x+3\right)^2=\left(x-x-3\right)\left(x+x+3\right)=-3\left(2x+3\right)\)
5: \(x^3+y^3+x+y\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+1\right)\)
6: \(x^3-y^3+x-y\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+1\right)\)
7: \(x^4-2x^3+x^2=x^2\cdot x^2-x^2\cdot2x+x^2\cdot1\)
\(=x^2\left(x^2-2x+1\right)=x^2\left(x-1\right)^2\)
8: \(5x^3+10x^2y+5xy^2\)
\(=5x\cdot x^2+5x\cdot2xy+5x\cdot y^2\)
\(=5x\left(x^2+2xy+y^2\right)=5x\left(x+y\right)^2\)
9: \(2xy-x^2-y^2+16\)
\(=16-\left(x^2-2xy+y^2\right)\)
\(=4^2-\left(x-y\right)^2=\left(4-x+y\right)\left(4+x-y\right)\)
10: \(2x^2+4x+2-2y^2\)
\(=2\left(x^2+2x+1-y^2\right)\)
\(=2\left[\left(x+1\right)^2-y^2\right]=2\left(x+1+y\right)\left(x+1-y\right)\)