Bài 44:
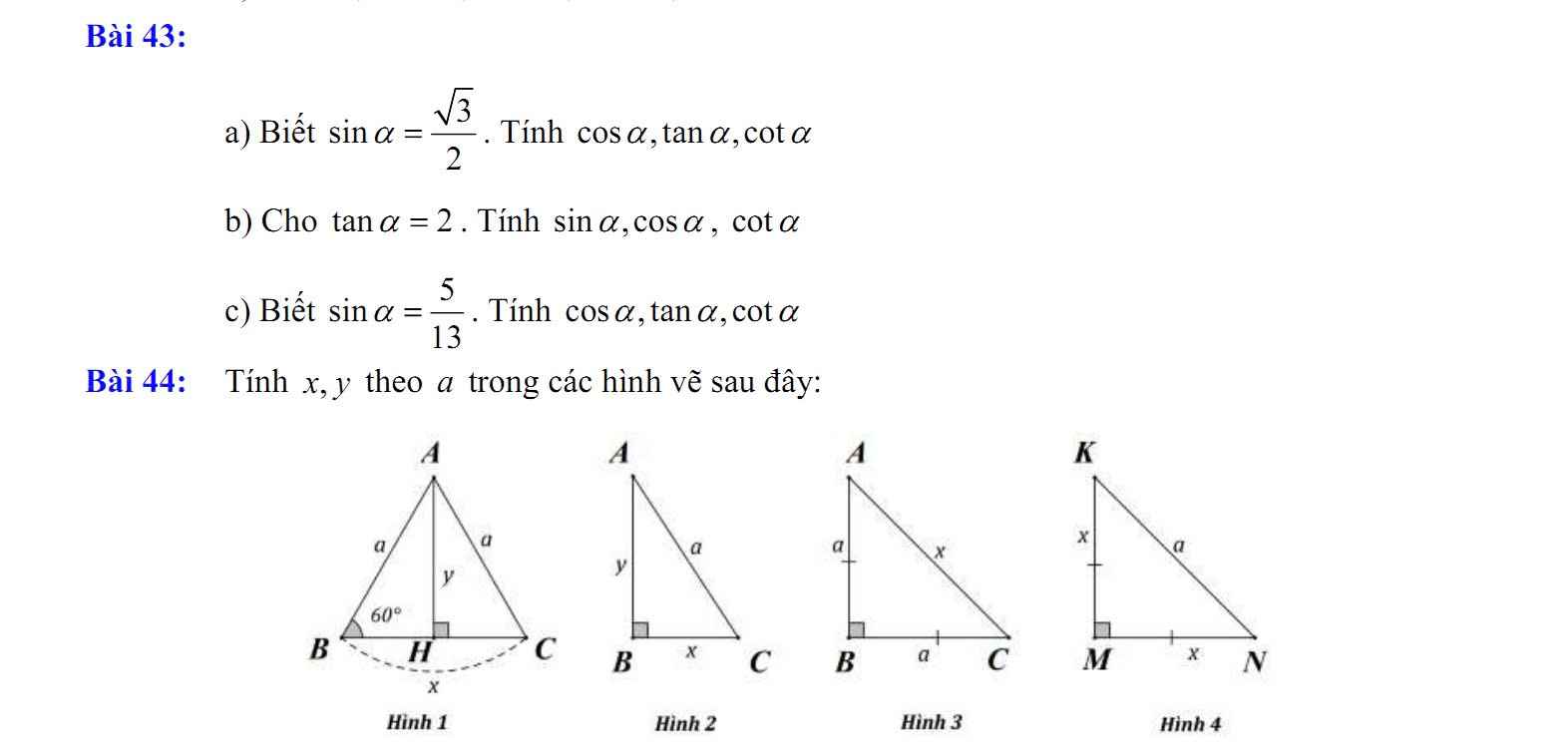
Hình 1: Xét ΔABC có AB=AC và \(\widehat{ABC}=60^0\)
nên ΔABC đều
=>x=BC=a
Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{y}{a}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(y=\dfrac{a\sqrt{3}}{2}\)
Hình 2: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(x^2+y^2=a^2\)
Hình 3: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(x^2=a^2+a^2=2a^2\)
=>\(x=a\sqrt{2}\)
Hình 4: ΔKMN vuông tại M
=>\(MN^2+MK^2=NK^2\)
=>\(x^2+x^2=a^2\)
=>\(x^2=\dfrac{a^2}{2}=\dfrac{2a^2}{4}\)
=>\(x=\sqrt{\dfrac{2a^2}{4}}=\dfrac{a\sqrt{2}}{2}\)
Bài 43:
a: \(sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\left(\dfrac{\sqrt{3}}{2}\right)^2=1-\dfrac{3}{4}=\dfrac{1}{4}\)
=>\(\left[{}\begin{matrix}cos\alpha=\dfrac{1}{2}\\cos\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
TH1: \(cos\alpha=\dfrac{1}{2}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{\sqrt{3}}\)
TH2: \(cos\alpha=-\dfrac{1}{2}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\sqrt{3}}{2}:\dfrac{-1}{2}=-\sqrt{3}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{-\sqrt{3}}=-\dfrac{1}{\sqrt{3}}\)
b:
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{2}\)
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2\alpha}=1+4=5\)
=>\(cos^2\alpha=\dfrac{1}{5}\)
=>\(\left[{}\begin{matrix}cos\alpha=\dfrac{1}{\sqrt{5}}\\cos\alpha=-\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
TH1: \(cos\alpha=\dfrac{1}{\sqrt{5}}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}\)
=>\(sin\alpha=\dfrac{1}{\sqrt{5}}\cdot2=\dfrac{2}{\sqrt{5}}\)
TH2: \(cos\alpha=-\dfrac{1}{\sqrt{5}}\)
\(sin\alpha=tan\alpha\cdot cos\alpha=-\dfrac{1}{\sqrt{5}}\cdot2=-\dfrac{2}{\sqrt{5}}\)
c: \(sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\left(\dfrac{5}{13}\right)^2=\dfrac{144}{169}=\left(\dfrac{12}{13}\right)^2\)
=>\(cos\alpha=\dfrac{12}{13}\) hoặc \(cos\alpha=-\dfrac{12}{13}\)
TH1: \(cos\alpha=\dfrac{12}{13}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)
\(cot\alpha=1:\dfrac{5}{12}=\dfrac{12}{5}\)
TH2: \(cos\alpha=-\dfrac{12}{13}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{5}{13}:\dfrac{-12}{13}=-\dfrac{5}{12}\)
\(cot\alpha=1:\dfrac{-5}{12}=-\dfrac{12}{5}\)