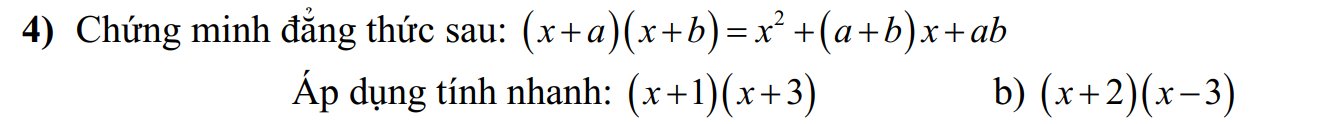Question

Answer 1

\(\left(x+a\right)\left(x+b\right)=x^2+bx+ax+ab=x^2+ax+bx+ab=x^2+\left(a+b\right)x+ab\left(dpcm\right)\)

Áp dụng :

a) \(\left(x+1\right)\left(x+3\right)=x^2+\left(1+3\right)x+1.3=x^2+4x+3\)

\(\left(x+2\right)\left(x-3\right)=x^2+\left(2-3\right)x+2.\left(-3\right)=x^2-x-6\)

 

Answer 2

\(\left(x+a\right)\left(x+b\right)=x^2+bx+ax+ab=x^2+\left(a+b\right)x+ab\) (đpcm)

Áp dụng:

\(\left(x+1\right)\left(x+3\right)=x^2+\left(1+3\right)x+1.3=x^2+4x+3\)

\(\left(x+2\right)\left(x-3\right)=x^2+\left(2-3\right)x+2.\left(-3\right)=x^2-x-6\)