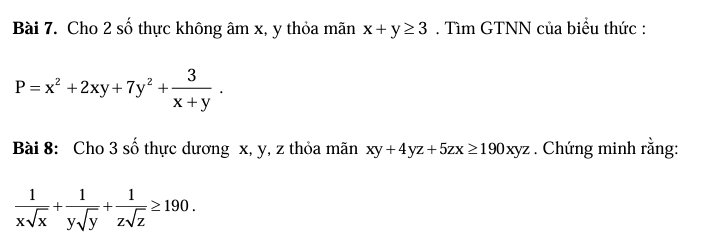7.
\(P=\left(x+y\right)^2+\dfrac{3}{x+y}+6y^2\ge\left(x+y\right)^2+\dfrac{3}{x+y}\)
\(P\ge\dfrac{\left(x+y\right)^2}{18}+\dfrac{3}{2\left(x+y\right)}+\dfrac{3}{2\left(x+y\right)}+\dfrac{17}{18}.\left(x+y\right)^2\)
\(P\ge3\sqrt[3]{\dfrac{9\left(x+y\right)^2}{18.2.2.\left(x+y\right)^2}}+\dfrac{17}{18}.3^2=10\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(3;0\right)\)
8.
\(xy+4yz+5zx\ge190xyz\Leftrightarrow\dfrac{4}{x}+\dfrac{5}{y}+\dfrac{1}{z}\ge190\)
Đặt \(\left(\dfrac{1}{\sqrt{x}};\dfrac{1}{\sqrt{y}};\dfrac{1}{\sqrt[]{z}}\right)=\left(a;b;c\right)\Rightarrow4a^2+5b^2+c^2\ge190\)
Gọi vế trái BĐT cần chứng minh là P
Ta có:
\(P=a^3+b^3+c^3\)
Áp dụng AM-GM:
\(a^3+a^3+64\ge3\sqrt[3]{64a^6}=12a^2\)
\(b^3+b^3+125\ge3\sqrt[3]{125b^6}=15b^2\)
\(c^3+c^3+1\ge3\sqrt[3]{c^6}=3c^2\)
Cộng vế:
\(2\left(a^3+b^3+c^3\right)+190\ge3\left(4a^2+5b^2+c^2\right)\ge3.190=570\)
\(\Rightarrow P\ge\dfrac{570-190}{2}=190\) (đpcm)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(4;5;1\right)\) hay \(\left(x;y;z\right)=\left(\dfrac{1}{16};\dfrac{1}{25};1\right)\)