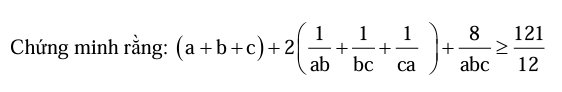Đặt vế trái là P:
\(P=\dfrac{13}{6}\left(\dfrac{a}{3}+\dfrac{b}{4}\right)+\dfrac{13}{24}\left(\dfrac{b}{2}+c\right)+\left(\dfrac{a}{18}+\dfrac{b}{24}+\dfrac{2}{ab}\right)+\left(\dfrac{b}{16}+\dfrac{c}{8}+\dfrac{2}{bc}\right)+\left(\dfrac{a}{9}+\dfrac{c}{6}+\dfrac{2}{ca}\right)+\left(\dfrac{a}{9}+\dfrac{b}{12}+\dfrac{c}{6}+\dfrac{8}{abc}\right)\)
\(\ge\dfrac{13}{6}.2\sqrt{\dfrac{ab}{12}}+\dfrac{13}{24}.2\sqrt{\dfrac{bc}{2}}+3\sqrt[3]{\dfrac{2ab}{18.24ab}}+3\sqrt[3]{\dfrac{2bc}{8.16bc}}+3\sqrt[3]{\dfrac{2ca}{54ca}}+4\sqrt[4]{\dfrac{8abc}{9.12.6.abc}}\)
\(=...\)
Đúng 0
Bình luận (0)
