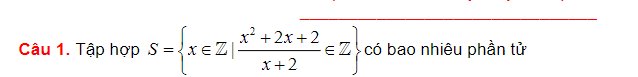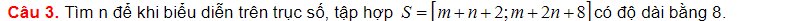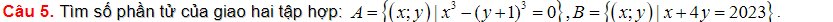Câu 1: Để \(\dfrac{x^2+2x+2}{x+2}\in Z\) thì \(x^2+2x+2⋮x+2\)
=>\(2⋮x+2\)
=>\(x+2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{-1;-3;0;-4\right\}\)
Vậy: S={-1;-3;0;-4}
=>S có 4 phần tử
Câu 5:
\(x^3-\left(y+1\right)^3=0\)
=>\(x^3=\left(y+1\right)^3\)
=>x=y+1
x+4y=2023
=>y+1+4y=2023
=>5y=2022
=>\(y=\dfrac{2022}{5}\)
=>\(x=\dfrac{2022}{5}+1=\dfrac{2027}{5}\)
Vậy: A giao B có 1 phần tử
Đúng 1
Bình luận (0)