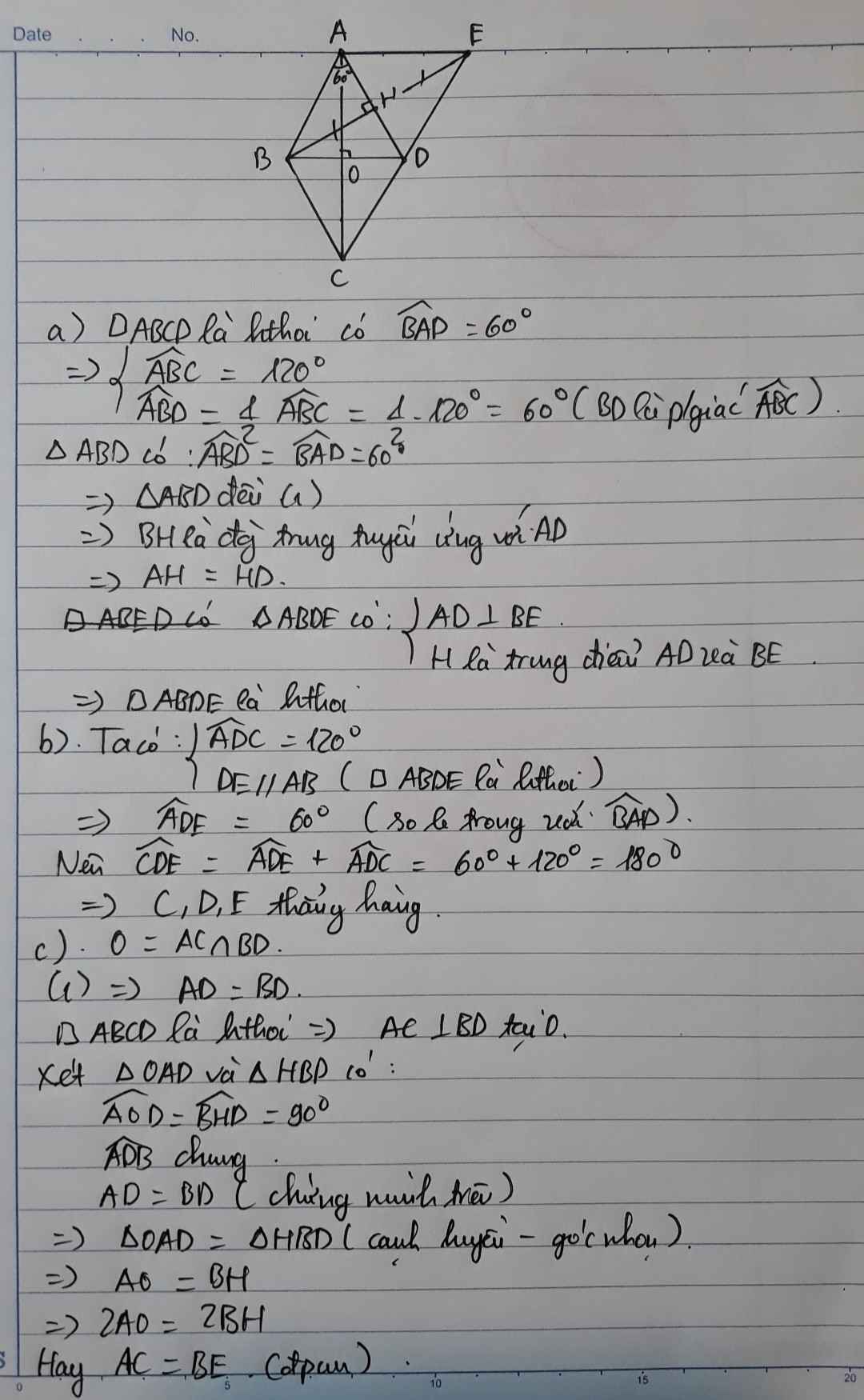a: Xét ΔABD có AB=AD và \(\widehat{BAD}=60^0\)
nên ΔABD đều
=>BA=BD
ΔBAD đều
mà BH là đường cao
nên H là trung điểm của AD
Xét tứ giác ABDE có
H là trung điểm chung của AD và BE
=>ABDE là hình bình hành
Hình bình hành ABDE có BA=BD
nên ABDE là hình thoi
b: ABDE là hình thoi
=>DE//AB
mà DC//AB
và DC,DE có điểm chung là D
nên C,D,E thẳng hàng
c:
ABCD là hình thoi
=>\(\widehat{ADC}+\widehat{DAB}=180^0\)(hai góc kề bù)
=>\(\widehat{ADC}=180^0-60^0=120^0\)
ABDE là hình thoi
=>AD là phân giác của góc BAE
=>\(\widehat{BAE}=2\cdot\widehat{BAD}=120^0\)
Xét ΔBAE có \(cosBAE=\dfrac{AB^2+AE^2-BE^2}{2\cdot AB\cdot AE}\)
=>\(\dfrac{AB^2+AB^2-BE^2}{2\cdot AB^2}=cos120=-\dfrac{1}{2}\)
=>\(2AB^2-BE^2=-AB^2\)
=>\(BE^2=3\cdot AB^2\)(1)
Xét ΔDAC có \(cosADC=\dfrac{DA^2+DC^2-AC^2}{2\cdot DA\cdot DC}\)
=>\(2BA^2-AC^2=2\cdot BA\cdot BA\cdot cos120=-BA^2\)
=>\(AC^2=3BA^2\)(2)
Từ (1),(2) suy ra BE=AC