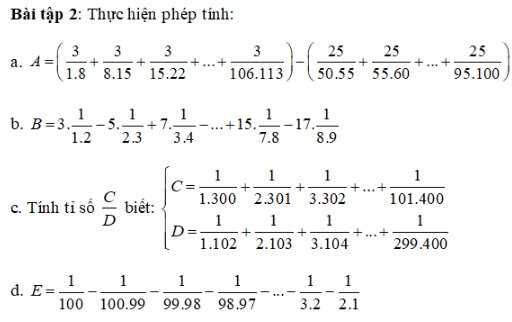a: \(A=\left(\dfrac{3}{1\cdot8}+\dfrac{3}{8\cdot15}+...+\dfrac{3}{106\cdot113}\right)-\left(\dfrac{25}{50\cdot55}+\dfrac{25}{55\cdot60}+...+\dfrac{25}{95\cdot100}\right)\)
\(=\dfrac{3}{7}\left(\dfrac{7}{1\cdot8}+\dfrac{7}{8\cdot15}+...+\dfrac{7}{106\cdot113}\right)-5\left(\dfrac{5}{50\cdot55}+\dfrac{5}{55\cdot60}+...+\dfrac{5}{95\cdot100}\right)\)
\(=\dfrac{3}{7}\left(1-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{15}+...+\dfrac{1}{106}-\dfrac{1}{113}\right)-5\left(\dfrac{1}{50}-\dfrac{1}{55}+\dfrac{1}{55}-\dfrac{1}{60}+...+\dfrac{1}{95}-\dfrac{1}{100}\right)\)
\(=\dfrac{3}{7}\left(1-\dfrac{1}{113}\right)-5\left(\dfrac{1}{50}-\dfrac{1}{100}\right)\)
\(=\dfrac{3}{7}\cdot\dfrac{112}{113}-5\cdot\dfrac{1}{100}=\dfrac{48}{113}-\dfrac{1}{20}=\dfrac{847}{2260}\)
b: \(B=3\cdot\dfrac{1}{1\cdot2}-5\cdot\dfrac{1}{2\cdot3}+7\cdot\dfrac{1}{3\cdot4}-...+15\cdot\dfrac{1}{7\cdot8}-17\cdot\dfrac{1}{8\cdot9}\)
\(=\dfrac{3}{1\cdot2}-\dfrac{5}{2\cdot3}+\dfrac{7}{3\cdot4}-...+\dfrac{15}{7\cdot8}-\dfrac{17}{8\cdot9}\)
\(=1+\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}+...+\dfrac{1}{7}+\dfrac{1}{8}-\dfrac{1}{8}-\dfrac{1}{9}\)
\(=1-\dfrac{1}{9}=\dfrac{8}{9}\)
d: \(E=\dfrac{1}{100}-\dfrac{1}{100\cdot99}-\dfrac{1}{99\cdot98}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{100}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)
\(=\dfrac{1}{100}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{100}-\left(1-\dfrac{1}{100}\right)=\dfrac{1}{100}-\dfrac{99}{100}=-\dfrac{98}{100}=-\dfrac{49}{50}\)