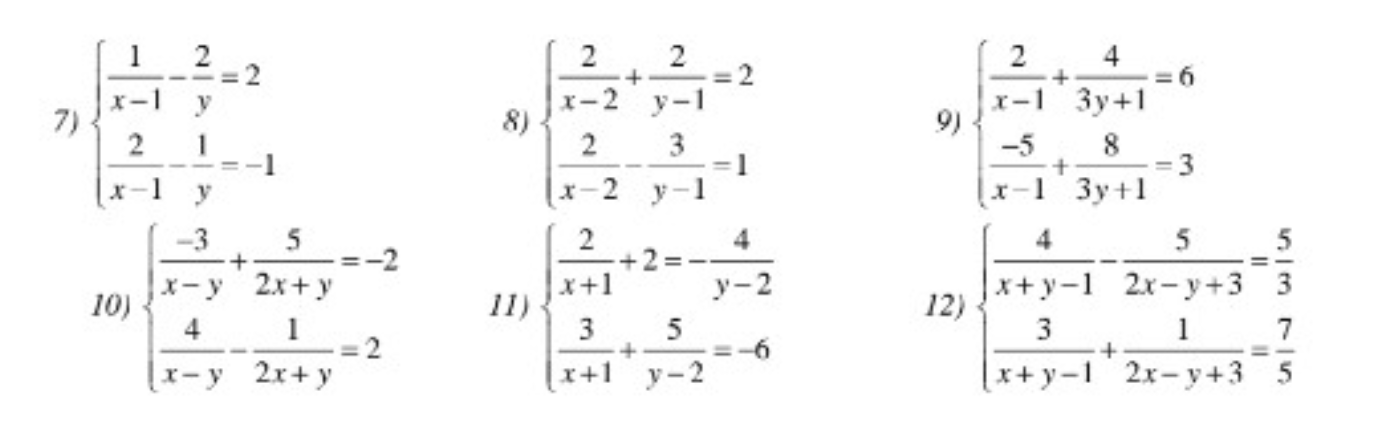7, \(\left\{{}\begin{matrix}\dfrac{1}{x-1}-\dfrac{2}{y}=2\\\dfrac{2}{x-1}-\dfrac{1}{y}=-1\end{matrix}\right.\)
Đặt \(\dfrac{1}{x-1}=a;\dfrac{1}{y}=b\)
\(\left\{{}\begin{matrix}a-2b=2\\2a-b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x-1}=-3\\\dfrac{1}{y}=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=-\dfrac{1}{3}\\y=-\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
-mấy câu sau tương tự nhé
12: ĐKXĐ: \(y\ne-x+1;y\ne2x+3\)
\(\left\{{}\begin{matrix}\dfrac{4}{x+y-1}-\dfrac{5}{2x-y+3}=\dfrac{5}{3}\\\dfrac{3}{x+y-1}+\dfrac{1}{2x-y+3}=\dfrac{7}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{12}{x+y-1}-\dfrac{15}{2x-y+3}=5\\\dfrac{12}{x+y-1}+\dfrac{4}{2x-y+3}=\dfrac{28}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{12}{x+y-1}-\dfrac{15}{2x-y+3}-\dfrac{12}{x+y-1}-\dfrac{4}{2x-y+3}=5-\dfrac{28}{5}\\\dfrac{4}{x+y-1}-\dfrac{5}{2x-y+3}=\dfrac{5}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{19}{2x-y+3}=-\dfrac{3}{5}\\\dfrac{4}{x+y-1}=\dfrac{5}{3}+\dfrac{5}{2x-y+3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3=\dfrac{95}{3}\\\dfrac{4}{x+y-1}=\dfrac{5}{3}+5:\dfrac{95}{3}=\dfrac{104}{57}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=\dfrac{95}{3}-3=\dfrac{95}{3}-\dfrac{9}{3}=\dfrac{86}{3}\\x+y-1=\dfrac{57}{26}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=\dfrac{86}{3}\\x+y=\dfrac{57}{26}+1=\dfrac{83}{26}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y+x+y=\dfrac{86}{3}+\dfrac{83}{26}\\x+y=\dfrac{83}{26}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2485}{234}\\y=\dfrac{83}{26}-\dfrac{2485}{234}=-\dfrac{869}{117}\end{matrix}\right.\)
11: ĐKXĐ: \(x\ne-1;y\ne2\)
\(\left\{{}\begin{matrix}\dfrac{2}{x+1}+2=-\dfrac{4}{y-2}\\\dfrac{3}{x+1}+\dfrac{5}{y-2}=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}+\dfrac{4}{y-2}=-2\\\dfrac{3}{x+1}+\dfrac{5}{y-2}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+1}+\dfrac{12}{y-2}=-6\\\dfrac{6}{x+1}+\dfrac{10}{y-2}=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x+1}+\dfrac{12}{y-2}-\dfrac{6}{x+1}-\dfrac{10}{y-2}=-6+12\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{y-2}=6\\\dfrac{1}{x+1}=-1-\dfrac{2}{y-2}=-1-6=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-2=\dfrac{1}{3}\\x+1=-\dfrac{1}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2+\dfrac{1}{3}=\dfrac{7}{3}\\x=-\dfrac{1}{7}-1=-\dfrac{8}{7}\end{matrix}\right.\left(nhận\right)\)
10: ĐKXĐ: \(y\ne x;y\ne-2x\)
\(\left\{{}\begin{matrix}\dfrac{-3}{x-y}+\dfrac{5}{2x+y}=-2\\\dfrac{4}{x-y}-\dfrac{1}{2x+y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{12}{x-y}+\dfrac{20}{2x+y}=-8\\\dfrac{12}{x-y}-\dfrac{3}{2x+y}=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{12}{x-y}+\dfrac{20}{2x+y}+\dfrac{12}{x-y}-\dfrac{3}{2x+y}=-8+6\\\dfrac{4}{x-y}-\dfrac{1}{2x+y}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{17}{2x+y}=-2\\\dfrac{4}{x-y}=\dfrac{1}{2x+y}+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=-\dfrac{2}{17}\\\dfrac{4}{x-y}=1:\dfrac{-2}{17}+2=-\dfrac{17}{2}+2=-\dfrac{13}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+y=-\dfrac{2}{17}\\x-y=4\cdot\dfrac{-2}{13}=-\dfrac{8}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y+x-y=-\dfrac{2}{17}-\dfrac{8}{13}\\x-y=-\dfrac{8}{13}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=\dfrac{-162}{221}\\y=x+\dfrac{8}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{54}{221}\\y=\dfrac{-54}{221}+\dfrac{8}{13}=\dfrac{82}{221}\end{matrix}\right.\)
7: ĐKXĐ: \(x\ne1;y\ne0\)
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}-\dfrac{2}{y}=2\\\dfrac{2}{x-1}-\dfrac{1}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x-1}-\dfrac{2}{y}=2\\\dfrac{4}{x-1}-\dfrac{2}{y}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x-1}-\dfrac{2}{y}-\dfrac{4}{x-1}+\dfrac{2}{y}=2+2\\\dfrac{1}{x-1}-\dfrac{2}{y}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{3}{x-1}=4\\\dfrac{2}{y}=\dfrac{1}{x-1}-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=-\dfrac{4}{3}\\\dfrac{2}{y}=1:\dfrac{-4}{3}-2=-\dfrac{3}{4}-2=-\dfrac{11}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{4}{3}+1=-\dfrac{1}{3}\\y=\dfrac{-4\cdot2}{11}=-\dfrac{8}{11}\end{matrix}\right.\left(nhận\right)\)
8: ĐKXĐ: \(x\ne2;y\ne1\)
\(\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{2}{y-1}=2\\\dfrac{2}{x-2}-\dfrac{3}{y-1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{2}{y-1}-\dfrac{2}{x-2}+\dfrac{3}{y-1}=2-1\\\dfrac{1}{x-2}+\dfrac{1}{y-1}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{y-1}=1\\\dfrac{1}{x-2}=1-\dfrac{1}{y-1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=5\\\dfrac{1}{x-2}=1-\dfrac{1}{5}=\dfrac{4}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=6\\x-2=\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=\dfrac{5}{4}+2=\dfrac{13}{4}\end{matrix}\right.\left(nhận\right)\)
9: ĐKXĐ: \(x\ne1;y\ne-\dfrac{1}{3}\)
\(\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{4}{3y+1}=6\\\dfrac{-5}{x-1}+\dfrac{8}{3y+1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-1}+\dfrac{8}{3y+1}=12\\\dfrac{-5}{x-1}+\dfrac{8}{3y+1}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x-1}+\dfrac{8}{3y+1}+\dfrac{5}{x-1}-\dfrac{8}{3y+1}=12-3\\\dfrac{1}{x-1}+\dfrac{2}{3y+1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x-1}=9\\\dfrac{2}{3y+1}=3-\dfrac{1}{x-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\dfrac{2}{3y+1}=3-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\3y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\left(nhận\right)\)