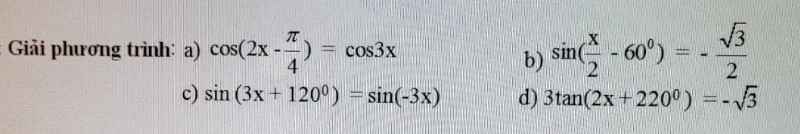a, \(cos\left(2x-\dfrac{\pi}{4}\right)=cos3x\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=3x+k2\pi\\2x-\dfrac{\pi}{4}=-3x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}-k2\pi\\x=\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
b, \(sin\left(\dfrac{x}{2}-60^0\right)=-\dfrac{\sqrt{3}}{2}=sin\left(-60^0\right)\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}-60^0=-60^0+k360^0\\\dfrac{x}{2}-60^0=120^0+k360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k720^0\\x=360^0+k720^0\end{matrix}\right.\)
c. \(sin\left(3x+120^0\right)=sin\left(-3x\right)\Leftrightarrow\left[{}\begin{matrix}3x+120^0=-3x+k360^0\\3x+120^0=180^0-3x+k360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-20^0+k60^0\\x=10^0+k60^0\end{matrix}\right.\)
d, \(3tan\left(2x+220^0\right)=-\sqrt{3}\Leftrightarrow tan\left(2x+220^0\right)=-\dfrac{\sqrt{3}}{3}\Leftrightarrow tan\left(2x+220^0\right)=tan\left(-30^0\right)\)
\(\Rightarrow2x+220^0=-30^0+k180^0\Leftrightarrow x=-125^0+k90^0\)