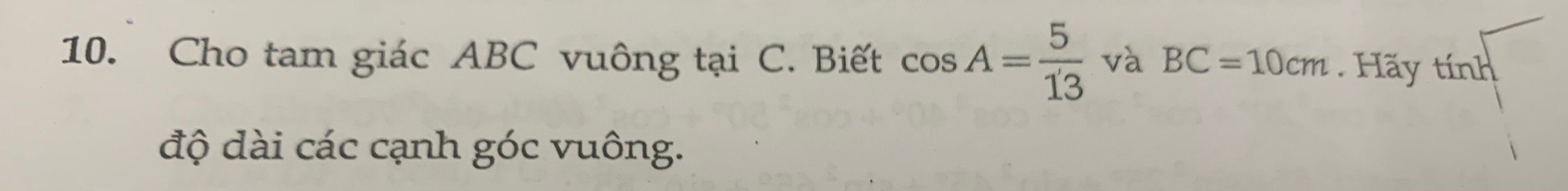Question

Answer 1

Xét ΔABC vuông tại C có \(cosA=\dfrac{CA}{AB}\)

=>\(\dfrac{CA}{AB}=\dfrac{5}{13}\)

=>\(\dfrac{CA}{5}=\dfrac{AB}{13}=k\)

=>CA=5k; AB=13k

ΔCAB vuông tại C

=>\(CA^2+CB^2=AB^2\)

=>\(\left(13k\right)^2-\left(5k\right)^2=CB^2=100\)

=>\(144k^2=100\)

=>\(k^2=\dfrac{100}{144}=\dfrac{25}{36}\)

=>\(k=\dfrac{5}{6}\)

=>\(CA=5\cdot\dfrac{5}{6}=\dfrac{25}{6}\left(cm\right);AB=13\cdot\dfrac{5}{6}=\dfrac{65}{6}\left(cm\right)\)