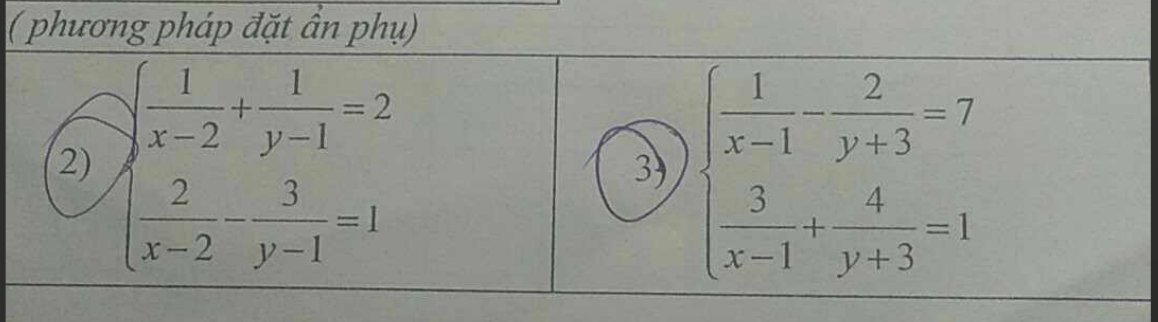
2: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne2\\y\ne1\end{matrix}\right.\)
Đặt \(\dfrac{1}{x-2}=a;\dfrac{1}{y-1}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a+b=2\\2a-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=4\\2a-3b=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+2b-2a+3b=4-1\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=3\\a=2-b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=\dfrac{3}{5}\\a=2-\dfrac{3}{5}=\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{7}{5}\\\dfrac{1}{y-1}=\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-2=\dfrac{5}{7}\\y-1=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2+\dfrac{5}{7}=\dfrac{19}{7}\\y=\dfrac{5}{3}+1=\dfrac{8}{3}\end{matrix}\right.\left(nhận\right)\)
3: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\y\ne-3\end{matrix}\right.\)
Đặt \(\dfrac{1}{x-1}=a;\dfrac{1}{y+3}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a-2b=7\\3a+4b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a-4b=14\\3a+4b=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5a=15\\a-2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\2b=a-7=3-7=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=\dfrac{1}{3}\\y+3=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1+\dfrac{1}{3}=\dfrac{4}{3}\\y=-2-\dfrac{1}{3}=-\dfrac{7}{3}\end{matrix}\right.\left(nhận\right)\)