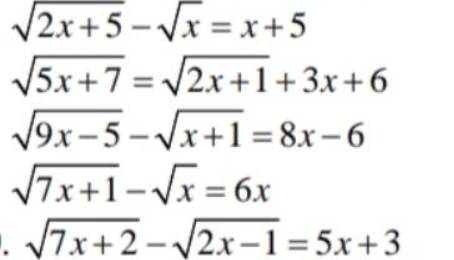a:
ĐKXĐ: x>=0
\(\sqrt{2x+5}-\sqrt{x}=x+5\)
=>\(\dfrac{2x+5-x}{\sqrt{2x+5}+\sqrt{x}}=x+5\)
=>\(\sqrt{2x+5}+\sqrt{x}=1\)
=>\(2x+5+x+2\sqrt{x\left(2x+5\right)}=1\)
=>\(\sqrt{4x\left(2x+5\right)}=1-3x-5=-3x-4\)
=>\(\left\{{}\begin{matrix}x< =-\dfrac{4}{3}\\\left(-3x-4\right)^2=4x\left(2x+5\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-\dfrac{4}{3}\\9x^2+24x+16=8x^2+20x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-\dfrac{4}{3}\\x^2+4x+16=0\end{matrix}\right.\)
=>\(x\in\varnothing\)
b: ĐKXĐ: x>=-1/2
\(\sqrt{5x+7}=\sqrt{2x+1}+3x+6\)
=>\(\sqrt{5x+7}-\sqrt{2x+1}=3x+6\)
=>\(\dfrac{5x+7-2x-1}{\sqrt{5x+7}+\sqrt{2x+1}}=3x+6\)
=>\(\sqrt{5x+7}+\sqrt{2x+1}=1\)
=>\(5x+7+2x+1+2\sqrt{\left(5x+7\right)\left(2x+1\right)}=1\)
=>\(\sqrt{4\left(10x^2+5x+14x+7\right)}=1-7x-8=-7x-7\)
=>\(\left\{{}\begin{matrix}-7x-7>=0\\\left(-7x-7\right)^2=4\left(10x^2+19x+7\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-1\\49x^2+98x+49=40x^2+76x+28\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-1\\9x^2+22x+21=0\end{matrix}\right.\)
=>\(x\in\varnothing\)
c: ĐKXĐ: x>=5/9
\(\sqrt{9x-5}-\sqrt{x+1}=8x-6\)
=>\(\dfrac{9x-5-x-1}{\sqrt{9x-5}+\sqrt{x+1}}=8x-6\)
=>\(\sqrt{9x-5}+\sqrt{x+1}=1\)
=>\(9x-5+x+1+2\sqrt{\left(9x-5\right)\left(x+1\right)}=1\)
=>\(10x-4+2\sqrt{9x^2+9x-5x-5}=1\)
=>\(\sqrt{4\left(9x^2+4x-5\right)}=1-10x+4=-10x+5\)
=>\(\left\{{}\begin{matrix}-10x+5>=0\\4\left(9x^2+4x-5\right)=\left(-10x+5\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-10x>=-5\\100x^2-100x+25=36x^2+16x-20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\64x^2-116x+45=0\end{matrix}\right.\)
=>\(x\in\varnothing\)
e:
ĐKXĐ: x>=1/2
\(\sqrt{7x+2}-\sqrt{2x-1}=5x+3\)
=>\(\dfrac{7x+2-2x+1}{\sqrt{7x+2}+\sqrt{2x-1}}=5x+3\)
=>\(\sqrt{7x+2}+\sqrt{2x-1}=1\)
=>\(7x+2+2x-1+2\sqrt{\left(7x+2\right)\left(2x-1\right)}=1\)
=>\(\sqrt{4\left(7x+2\right)\left(2x-1\right)}=1-9x-1=-9x\)
=>\(\left\{{}\begin{matrix}x< =0\\\left(-9x\right)^2=4\left(7x+2\right)\left(2x-1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =0\\81x^2=4\left(14x^2-3x-2\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =0\\25x^2+12x+8=0\end{matrix}\right.\)
=>\(x\in\varnothing\)