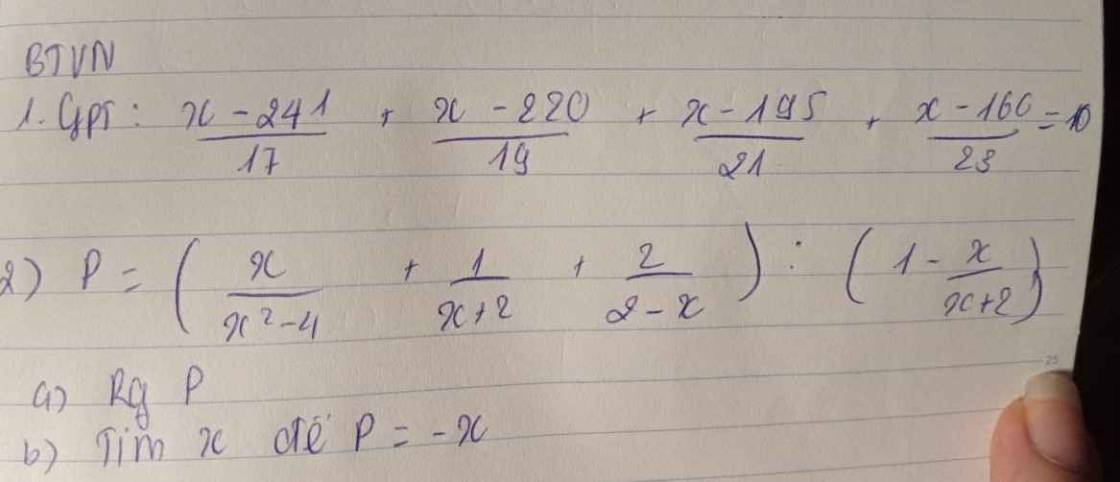Bài 2:
a. ĐKXĐ: $x\neq \pm 2$
\(P=\left[\frac{x}{(x-2)(x+2)}+\frac{x-2}{(x+2)(x-2)}-\frac{2(x+2)}{(x-2)(x+2)}\right]:\frac{2}{x+2}\\ =\frac{x+(x-2)-2(x+2)}{(x-2)(x+2)}.\frac{x+2}{2}\\ =\frac{-6}{(x-2)(x+2)}.\frac{x+2}{2}=\frac{3}{2-x}\)
b.
Để $P=-x\Leftrightarrow \frac{3}{2-x}=-x$
$\Rightarrow 3=x(x-2)$
$\Leftrightarrow x^2-2x-3=0$
$\Leftrightarrow (x+1)(x-3)=0$
$\Leftrightarrow x+1=0$ hoặc $x-3=0$
$\Leftrightarrow x=-1$ hoặc $x=3$ (tm)
Bài 1:
PT $\Leftrightarrow (\frac{x-241}{17}-1)+(\frac{x-220}{19}-2)+(\frac{x-195}{21}-3)+(\frac{x-160}{23}-4)=0$
$\Leftrightarrow \frac{x-258}{17}+\frac{x-258}{19}+\frac{x-258}{21}+\frac{x-258}{23}=0$
$\Leftrightarrow (x-258)\left(\frac{1}{17}+\frac{1}{19}+\frac{1}{21}+\frac{1}{23})=0$
$\Leftrightarrow x-258=0$
$\Leftrightarrow x=258$
2:ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
a: \(P=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}+\dfrac{2}{2-x}\right):\left(1-\dfrac{x}{x+2}\right)\)
\(=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}-\dfrac{2}{x-2}\right):\dfrac{x+2-x}{x+2}\)
\(=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{2}\)
\(=\dfrac{-6}{2\left(x-2\right)}=\dfrac{-3}{x-2}\)
b: Để P=-x thì -x(x-2)=-3
=>x(x-2)=3
=>\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)