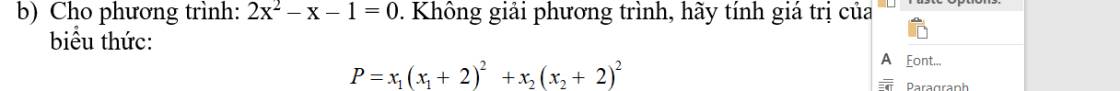Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=x_1\left(x_1+2\right)^2+x_2\left(x_2+2\right)^2\)
\(=x_1\left(x_1^2+4x_1+4\right)+x_2\left(x_2^2+4x_2+4\right)\)
\(=x_1^3+x_2^3+4\left(x_1^2+x_2^2\right)+4\left(x_1+x_2\right)\)
\(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+4\left(x_1+x_2\right)^2-8x_1x_2+4\left(x_1+x_2\right)\)
\(=\left(\dfrac{1}{2}\right)^3-3.\left(-\dfrac{1}{2}\right).\dfrac{1}{2}+4.\left(\dfrac{1}{2}\right)^2-8.\left(-\dfrac{1}{2}\right)+4.\dfrac{1}{2}\)
\(=\dfrac{63}{8}\)
Đúng 1
Bình luận (0)
