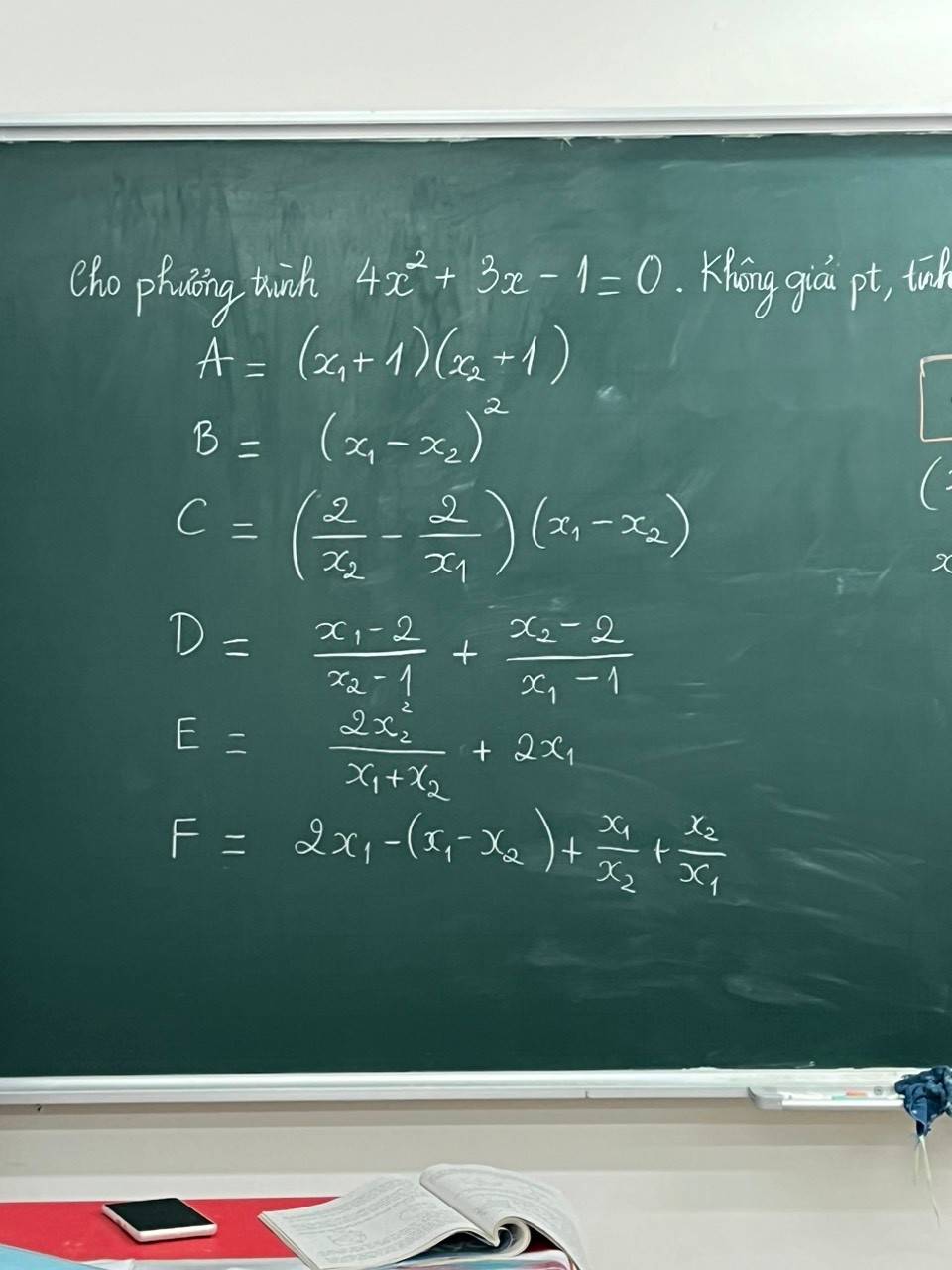Do a.c = 4.(-1) = -4 < 0 nên phương trình luôn có hai nghiệm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = -3
x₁x₂ = -1/4
A = (x₁ + 1)(x₂ + 1)
= x₁x₂ + x₁ + x₂ + 1
= -1/4 - 3 + 1
= -9/4
--------
B = (x₁ - x₂)²
= x₁² - 2x₁x₂ + x₂²
= x₁² + 2x₁x₂ + x₁² - 4x₁x₂
= (x₁ + x₂)² - 4x₁x₂
= (-3)² - 4.(-1/4)
= 9 + 1
= 10
--------
C = (2/x₁ - 2/x₂)(x₁ - x₂)
= [(2x₁ - 2x₂)/(x₁x₂)](x₁ - x₂)
= 2(x₁ - x₂)²/(x₁x₂)
= 2([(x₁ + x₂)² - 4x₁x₂]/(x₁x₂)
= 2.[(-3)² - 4.(-1/4)]/(-1/4)
= 2.10.(-4)
= -80
--------
D = (x₁ - 2)/(x₂ - 1) + (x₂ - 2)/(x₁ - 1)
= [(x₁ - 2)(x₁ - 1) + (x₂ - 2)(x₂ - 1)]/[(x₁ - 1)(x₂ - 1)]
= (x₁² - x₁ - 2x₁ + 2 + x₂² - x₂ - 2x₂ + 2)/(x₁x₂ - x₁ - x₂ + 1)
= [(x₁ + x₂)² - 2x₁x₂ - 2(x₁ + x₂) + 4]/[(x₁x₂ - (x₁ + x₂) + 1]
= [(-3)² - 2.(-1/4) - 2.(-3) + 4]/[-1/4 - (-3) + 1]
= (9 + 1/2 + 6 + 4)/(-1/4 + 3 + 1)
= 26/5
--------
E = 2x₂²/(x₁ + x₂) + 2x₁
= [2x₂² + 2x₁(x₁ + x₂)]/(x₁ + x₂)
= (2x₂² + 2x₁² + 2x₁x₂)/(x₁ + x₂)
= [2(x₁² + x₂²) + 2x₁x₂]/(x₁ + x₂)
= {2[(x₁ + x₂)² - 2x₁x₂] + 2x₁x₂}/(x₁ + x₂)
= {2[(-3)² - 2.(-1/4)] + 2.(-1/4)]}/(-3)
= (18 + 1 - 1/2)/(-3)
= -37/6
--------
F = 2x₁ - (x₁ - x₂) + x₁/x₂ + x₂/x₁
= 2x₁ - x₁ + x₂ + (x₁ + x₂)/(x₁x₂)
= x₁ + x₂ + (x₁ + x₂)/(x₁x₂)
= -3 + (-3)/(-1/4)
= 9