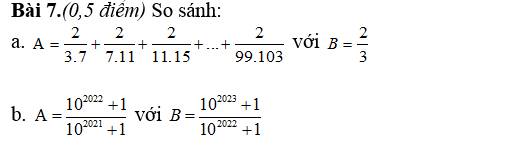a: \(A=\dfrac{2}{3\cdot7}+\dfrac{2}{7\cdot11}+...+\dfrac{2}{99\cdot103}\)
\(=\dfrac{1}{2}\left(\dfrac{4}{3\cdot7}+\dfrac{4}{7\cdot11}+...+\dfrac{4}{99\cdot103}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{99}-\dfrac{1}{103}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{103}\right)=\dfrac{1}{2}\cdot\dfrac{100}{309}=\dfrac{50}{309}< \dfrac{50}{75}=\dfrac{2}{3}\)
=>A<B
b: \(\dfrac{A}{10}=\dfrac{10^{2022}+1}{10^{2022}+10}=1-\dfrac{9}{10^{2022}+10}\)
\(\dfrac{B}{10}=\dfrac{10^{2023}+1}{10^{2023}+10}=1-\dfrac{9}{10^{2023}+10}\)
Vì \(10^{2022}+10< 10^{2023}+10\)
nên \(\dfrac{9}{10^{2022}+10}>\dfrac{9}{10^{2023}+10}\)
=>\(-\dfrac{9}{10^{2022}+10}< -\dfrac{9}{10^{2023}+10}\)
=>\(-\dfrac{9}{10^{2022}+10}+1< -\dfrac{9}{10^{2023}+10}+1\)
=>\(\dfrac{A}{10}< \dfrac{B}{10}\)
=>A<B