a: Vì \(y=x^2\) có a=1>0
nên hàm số \(y=x^2\) đồng biến khi x>0 và nghịch biến khi x<0
b: 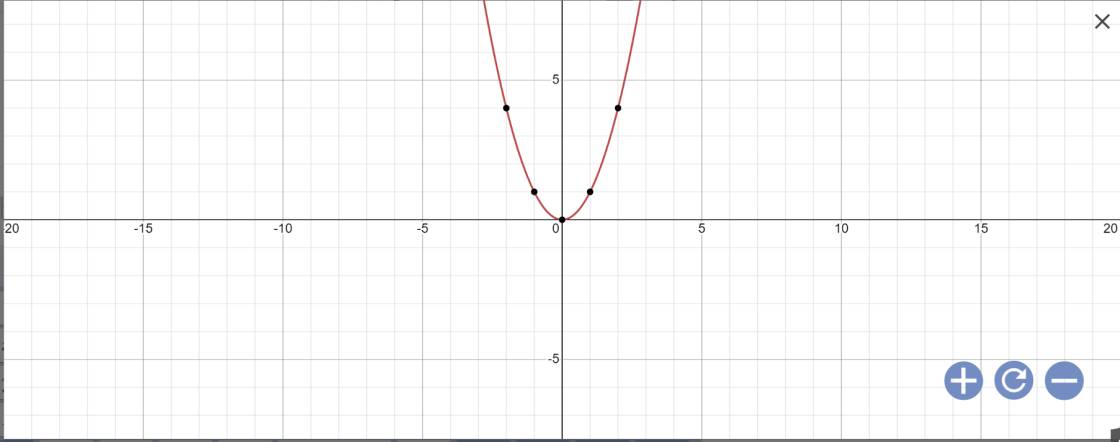
c: Thay x=3 vào \(y=x^2\), ta được:
\(y=3^2=9\)
=>E(3;9) thuộc (P)
Thay x=-3 vào (P), ta được:
\(y=\left(-3\right)^2=9\)
=>F(-3;-9) không thuộc (P)
d: Thay x=4 vào (P), ta được:
\(y=4^2=16\)
vậy: G(4;16)
e: Thay \(y=3\) vào (P), ta được:
\(x^2=3\)
=>\(\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\)
Vậy: \(H\left(\sqrt{3};3\right);K\left(-\sqrt{3};3\right)\)
g: Thay x=1/2 và y=m vào (P), ta được:
\(m=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
h: Thay x=n-1 và y=4n-4 vào (P), ta được:
\(\left(n-1\right)^2=4n-4\)
=>\(n^2-2n+1-4n+4=0\)
=>\(n^2-6n+5=0\)
=>(n-1)(n-5)=0
=>\(\left[{}\begin{matrix}n=1\\n=5\end{matrix}\right.\)



