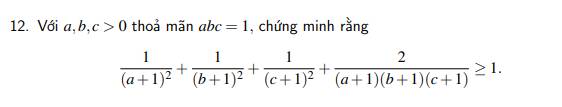Đặt vế trái BĐT cần c/m là P
Bunhiacopxki:
\(\left(a+b\right)\left(a+\dfrac{1}{b}\right)\ge\left(a+1\right)^2\Rightarrow\dfrac{1}{\left(a+1\right)^2}\ge\dfrac{1}{\left(a+b\right)\left(a+\dfrac{1}{b}\right)}=\dfrac{b}{\left(a+b\right)\left(ab+1\right)}\)
Tương tự: \(\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{a}{\left(a+b\right)\left(ab+1\right)}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{a+b}{\left(a+b\right)\left(ab+1\right)}=\dfrac{1}{ab+1}\)
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có ít nhất 2 số cùng phía so với 1. Ko mất tính tổng quát, giả sử đó là a và b
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\Rightarrow ab+1\ge a+b\)
\(\Rightarrow2\left(ab+1\right)\ge ab+a+b+1\)
\(\Rightarrow2\left(ab+1\right)\ge\left(a+1\right)\left(b+1\right)\)
\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{1}{\left(ab+1\right)\left(c+1\right)}\)
\(\Rightarrow P\ge\dfrac{1}{ab+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{1}{\left(ab+1\right)\left(c+1\right)}=\dfrac{c}{c+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{c}{\left(c+1\right)\left(c+1\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)