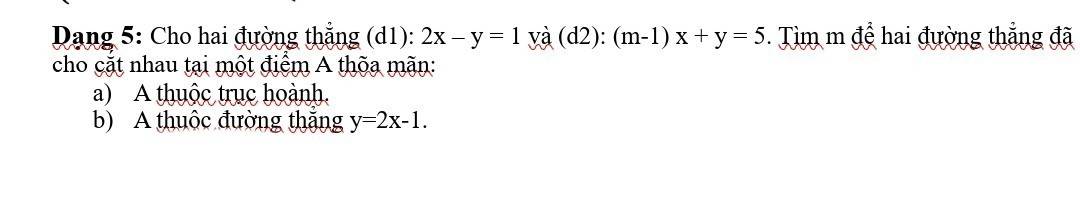a: (d1): 2x-y=1
=>y=2x-1
(d2): (m-1)x+y=5
=>y=-(m-1)x+5
Để (d1) và (d2) cắt nhau tại điểm A thuộc trục hoành thì
\(\left\{{}\begin{matrix}-\left(m-1\right)\ne2\\\dfrac{-\left(-1\right)}{2}=\dfrac{-5}{-\left(m-1\right)}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne-1\\\dfrac{1}{2}=\dfrac{5}{m-1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\m-1=10\end{matrix}\right.\)
=>m=11
b: Phương trình hoành độ giao điểm của (d1) và đường thẳng y=2x-1 là:
2x-1=2x-1
=>0x=0(luôn đúng)
Vậy: Khi \(m\ne-1\) thì (d1) và (d2) cắt nhau tại điểm A thuộc đường thẳng y=2x-1
Đúng 2
Bình luận (0)
