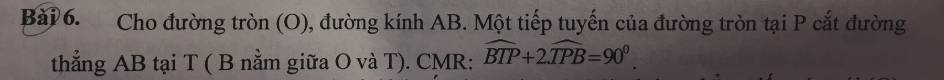Do PT là tiếp tuyến \(\Rightarrow\widehat{OPT}=90^0\)
\(\widehat{TPB}\) là góc tạo bởi tiếp tuyến và dây cung PB
\(\Rightarrow\widehat{TPB}=\dfrac{1}{2}sđ\stackrel\frown{BOP}=\dfrac{1}{2}\widehat{BOP}\)
\(\Rightarrow2.\widehat{TPB}=\widehat{BOP}\)
Trong tam giác OPT ta có:
\(\widehat{BOP}+\widehat{OPT}+\widehat{BTP}=180^0\)
\(\Leftrightarrow2\widehat{TPB}+90^0+\widehat{BTP}=180^0\)
\(\Leftrightarrow\widehat{BTP}+2\widehat{TPB}=90^0\)
Đúng 2
Bình luận (0)
