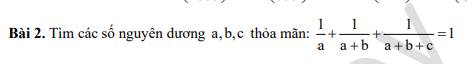Ta có:
\(\dfrac{1}{a+b+c}< \dfrac{1}{a+b}< \dfrac{1}{a}\Rightarrow\dfrac{1}{a}+\dfrac{1}{a+b}+\dfrac{1}{a+b+c}< \dfrac{3}{a}\)
\(\Rightarrow\dfrac{3}{a}>1\Rightarrow a< 3\)
Mà a nguyên dương nên \(a=1\) hoặc \(a=2\)
- Với \(a=1\) thay vào pt ban đầu:
\(\dfrac{1}{1}+\dfrac{1}{b+1}+\dfrac{1}{b+c+1}=1\Rightarrow\dfrac{1}{b+1}+\dfrac{1}{b+c+1}=0\) (vô lý do vế trái dương)
- Với \(a=2\) thay vào pt đầu:
\(\dfrac{1}{2}+\dfrac{1}{b+2}+\dfrac{1}{b+c+2}=1\Rightarrow\dfrac{1}{b+2}+\dfrac{1}{b+c+2}=\dfrac{1}{2}\) (1)
Do \(\dfrac{1}{b+2}>\dfrac{1}{b+c+2}\Rightarrow\dfrac{1}{b+2}+\dfrac{1}{b+c+2}< \dfrac{2}{b+2}\)
\(\Rightarrow\dfrac{2}{b+2}>\dfrac{1}{2}\Rightarrow b+2< 4\)
\(\Rightarrow b< 2\)
Mà b nguyên dương \(\Rightarrow b=1\)
Thay vào (1) \(\Rightarrow\dfrac{1}{3}+\dfrac{1}{c+3}=\dfrac{1}{2}\Rightarrow\dfrac{1}{c+3}=\dfrac{1}{6}\)
\(\Rightarrow c+3=6\Rightarrow c=3\)
Vậy \(\left(a;b;c\right)=\left(2;1;3\right)\)