Question

  

Answer 1

a: Đặt \(3x^2+x+1=0\)

\(\Delta=1^2-4\cdot3\cdot1=1-12=-11< 0\)

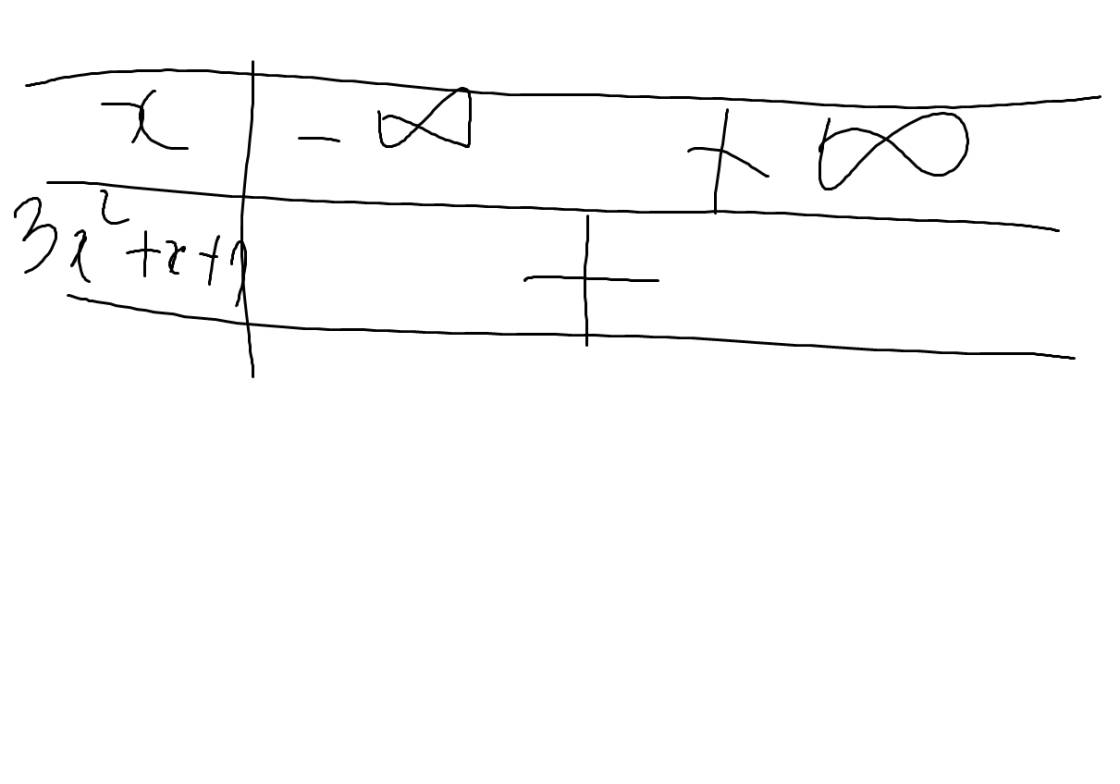
Vì Δ<0 và 3>0 nên \(3x^2+x+1>0\forall x\)

Bảng xét dấu:

b: Đặt \(x^2-5x+4=0\)

=>(x-1)(x-4)=0

=>\(\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\)

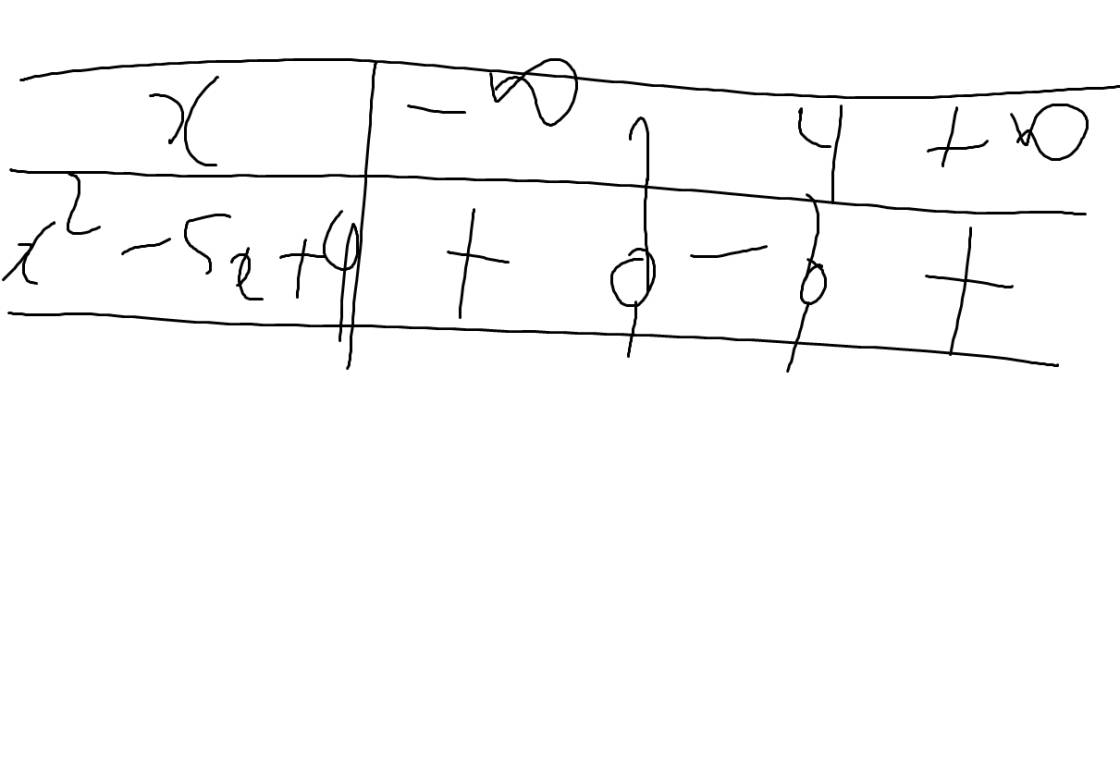
=>\(\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)

Bảng xét dấu:

c: Đặt \(-x^2+x-5=0\)

\(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-5\right)\)

\(=1-4\cdot5=1-20=-19< 0\)

Vì Δ<0 và -1<0

nên \(-x^2+x-5< 0\forall x\)

Bảng xét dấu:

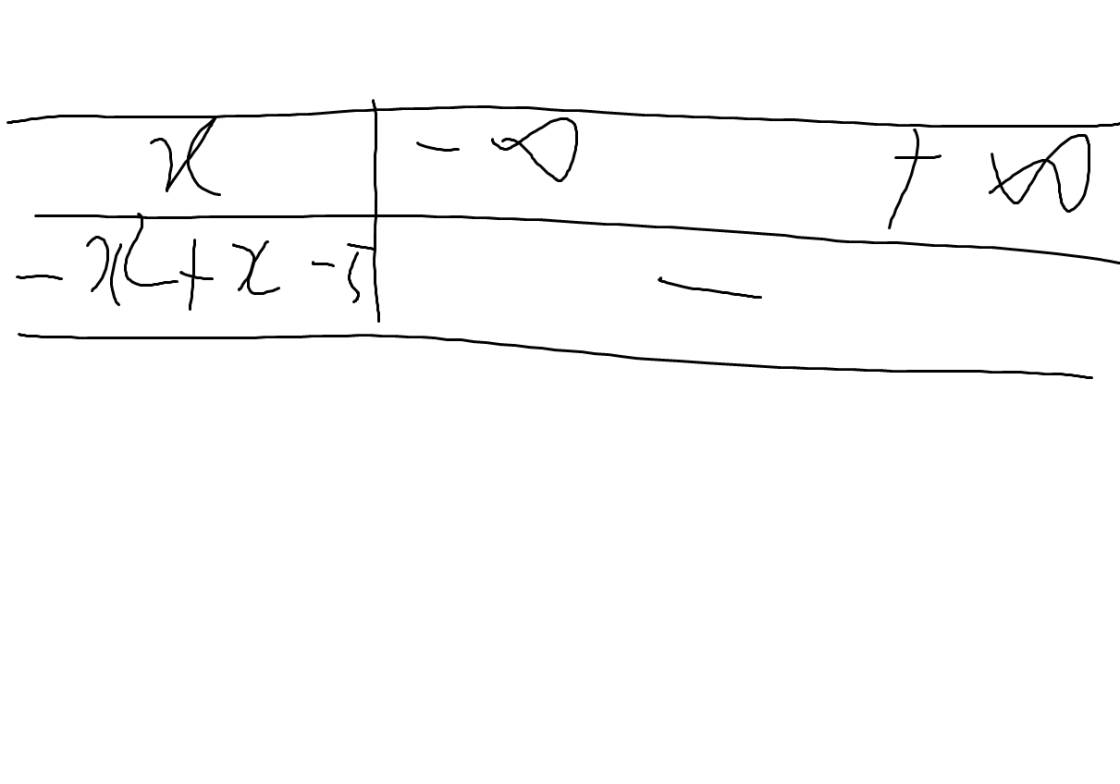
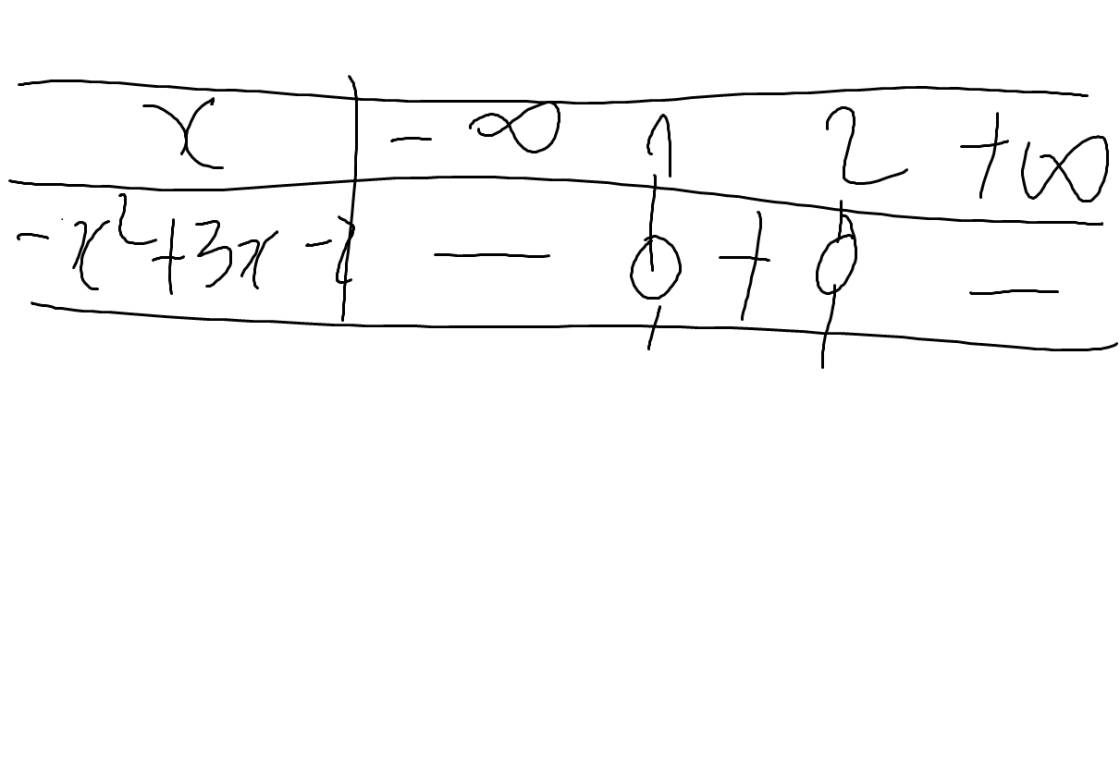
d: Đặt \(-x^2+3x-2=0\)

=>\(x^2-3x+2=0\)

=>(x-1)(x-2)=0

=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

Bảng xét dấu: