Xét trường hợp M nằm ngoài đường tròn:
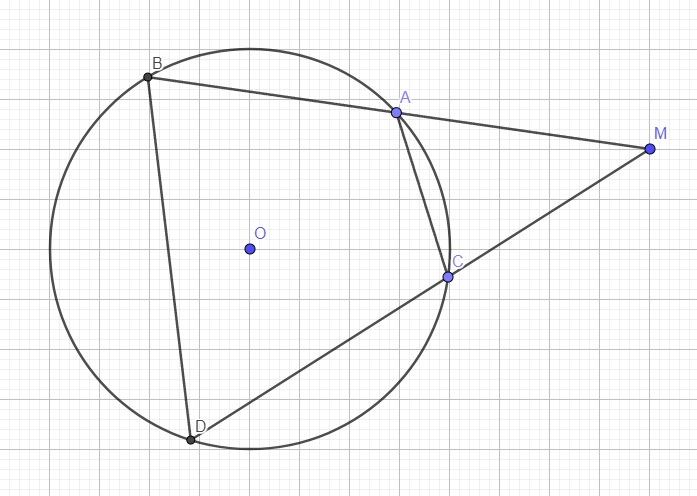
Tứ giác ABDC nội tiếp (O) \(\Rightarrow\widehat{BAC}+\widehat{BDC}=180^0\)
Mà \(\widehat{BAC}+\widehat{MAC}=180^0\) (hai góc kề bù)
\(\Rightarrow\widehat{BDC}=\widehat{MAC}\)
Xét 2 tam giác MAC và MDB có:
\(\left\{{}\begin{matrix}\widehat{AMC}\text{ chung}\\\widehat{MAC}=\widehat{BDC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta MAC\sim\Delta MDB\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MB}\Rightarrow MA.MB=MC.MD\)
Trường hợp M nằm trong đường tròn chứng minh tương tự:
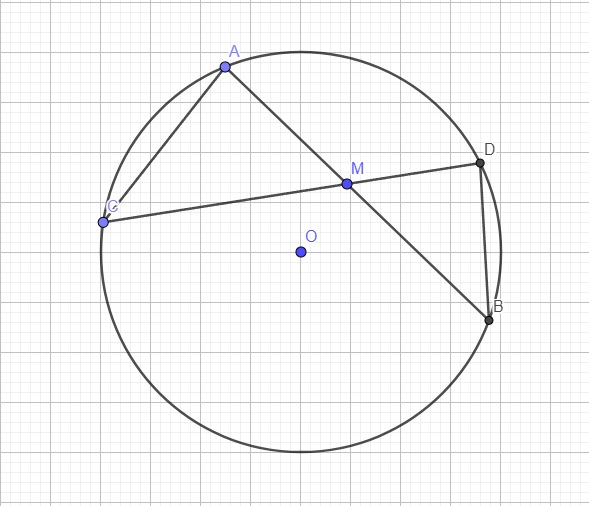
Xét hai tam giác MAC và MDB có:
\(\left\{{}\begin{matrix}\widehat{AMC}=\widehat{DMB}\left(\text{đối đỉnh}\right)\\\widehat{ACM}=\widehat{DBM}\left(\text{cùng chắn AD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDB\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MB}\Rightarrow MA.MB=MC.MD\)




