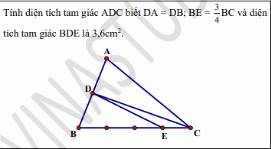
\(BE=\dfrac{3}{4}BC\)
=>\(S_{DBE}=\dfrac{3}{4}\cdot S_{DBC}\)
=>\(S_{DBC}=\dfrac{4}{3}\cdot3,6=4,8\left(cm^2\right)\)
DA=DB
D,A,B thẳng hàng
Do đó: D là trung điểm của AB
=>\(BD=\dfrac{1}{2}BA\)
=>\(S_{BDC}=\dfrac{1}{2}\cdot S_{BAC}\)
=>\(S_{BAC}=2\cdot4,8=9,6\left(cm^2\right)\)



 4 và 5
4 và 5