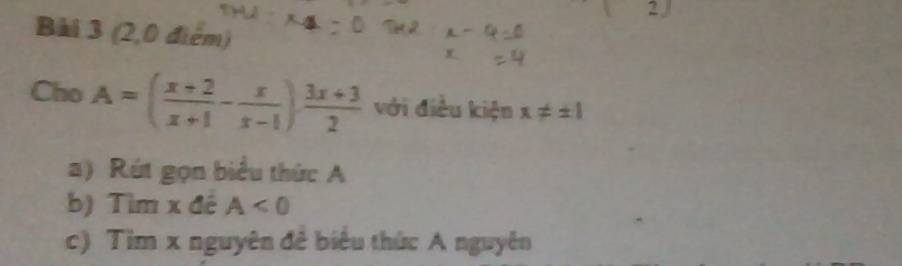Question

Answer 1

a: \(A=\left(\dfrac{x+2}{x+1}-\dfrac{x}{x-1}\right)\cdot\dfrac{3x+3}{2}\)

\(=\dfrac{\left(x+2\right)\left(x-1\right)-x\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{3x+3}{2}\)

\(=\dfrac{x^2+x-2-x^2-x}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{3\left(x+1\right)}{2}\)

\(=\dfrac{-2}{x-1}\cdot\dfrac{3}{2}=-\dfrac{3}{x-1}\)

b: A<0

=>\(-\dfrac{3}{x-1}< 0\)

=>x-1>0

=>x>1

c: Để A là số nguyên thì \(-3⋮x-1\)
=>\(x-1\inƯ\left(-3\right)\)

=>\(x-1\in\left\{1;-1;3;-3\right\}\)

=>\(x\in\left\{2;0;4;-2\right\}\)