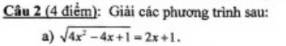\(\sqrt{4x^2-4x+1}=2x+1\\ \Leftrightarrow\sqrt{\left(2x+1\right)^2}=2x+1\\ \Leftrightarrow\left|2x+1\right|=2x+1\)
\(TH_1:2x+1>0\Leftrightarrow x>-\dfrac{1}{2}\\ 2x+1=2x+1\left(LD\forall x\right)\)
\(TH_2:2x+1\le0\Leftrightarrow x\le-\dfrac{1}{2}\\ -2x-1=2x+1\\ \Leftrightarrow-4x=2\\ \Leftrightarrow x=-\dfrac{1}{2}\left(tm\right)\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(\sqrt{4x^2-4x+1}=2x+1\)
=>\(\sqrt{\left(2x-1\right)^2}=2x+1\)
=>\(\left\{{}\begin{matrix}2x+1>=0\\\left(2x+1\right)^2=\left(2x-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{2}\\\left(2x+1-2x+1\right)\left(2x+1+2x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{2}\\4x=0\end{matrix}\right.\Leftrightarrow x=0\left(nhận\right)\)
√4x2−4x+1=2x+1
⇔√(2x-1)2=2x+1
⇔(2x-1)=2x+1
⇔1-2x=2x+1
⇔ -2x-2x=0
⇔-4x=0
⇔x=0