Question

Answer 1

Bài 4:

1: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2+144=400\)

=>\(AC^2=256\)

=>\(AC=\sqrt{256}=16\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

=>\(AH\cdot20=12\cdot16=192\)

=>AH=9,6(cm)

2:

ΔMNP vuông tại P

=>\(PM^2+PN^2=MN^2\)

=>\(PM^2+21^2=35^2\)

=>\(PM^2=35^2-21^2=784\)

=>PM=28(cm)

Xét ΔMNP vuông tại P có \(tanM=\dfrac{NP}{PM}\)

=>\(tanM=\dfrac{21}{28}=\dfrac{3}{4}\)

Bài 5:

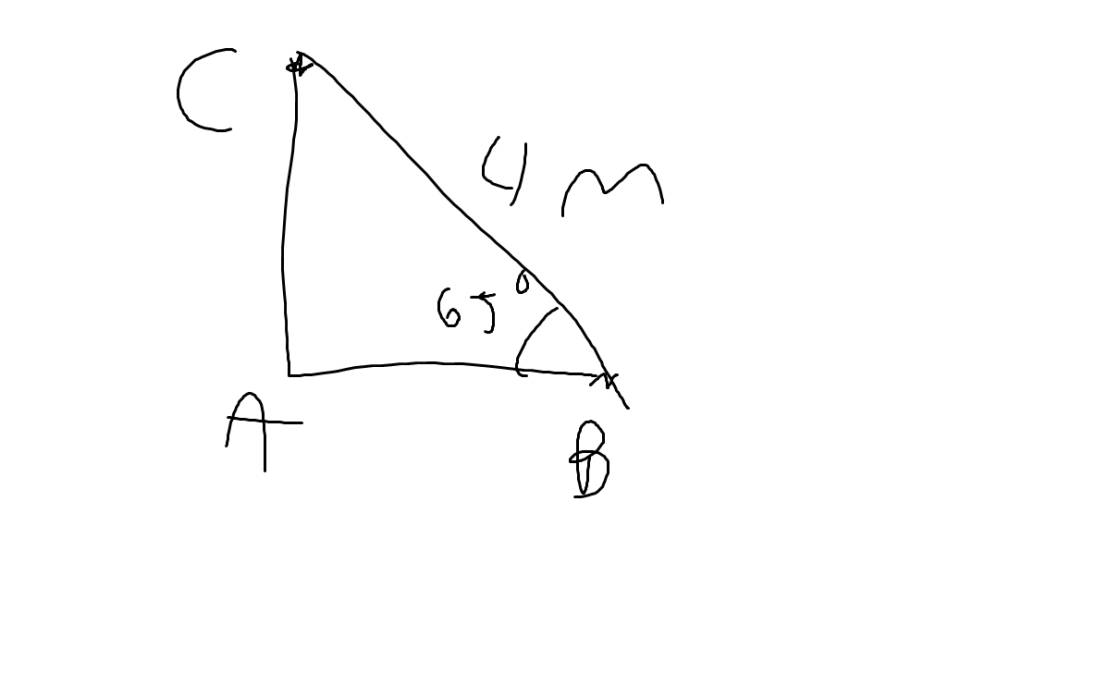
Gọi AC là khoảng cách từ đỉnh thang đến chân tường, AB là khoảng cách từ chân thang đến chân tường

Theo đề, ta có: AB\(\perp\)AC tại A; BC=4m; \(\widehat{B}=65^0\)

Xét ΔABC vuông tại A có

\(cosB=\dfrac{BA}{BC}\)

=>\(BA=4\cdot cos65\simeq1,69\left(m\right)\)