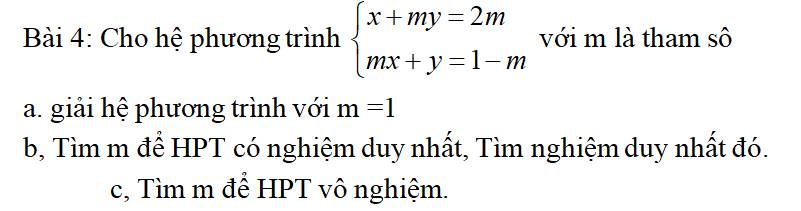a: Khi m=1 thì hệ phương trình sẽ là:
\(\left\{{}\begin{matrix}x+y=2\\x+y=1-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=2\left(loại\right)\\x+y=2\end{matrix}\right.\)
Vậy: Hệ vô nghiệm
b: Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}< >\dfrac{m}{1}\)
=>\(m^2< >1\)
=>\(m\notin\left\{1;-1\right\}\)
\(\left\{{}\begin{matrix}x+my=2m\\mx+y=1-m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}mx+m^2y=2m^2\\mx+y=1-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2-1\right)=2m^2-1+m\\x+my=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{2m^2+m-1}{m^2-1}=\dfrac{\left(m+1\right)\left(2m-1\right)}{\left(m+1\right)\left(m-1\right)}=\dfrac{2m-1}{m-1}\\x=2m-my=2m-\dfrac{m\left(2m-1\right)}{m-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{2m-1}{m-1}\\x=\dfrac{2m^2-2m-2m^2+m}{m-1}=-\dfrac{m}{m-1}\end{matrix}\right.\)
c: Để hệ vô nghiệm thì \(\dfrac{1}{m}=\dfrac{m}{1}< >\dfrac{2m}{1-m}\)
=>\(\left\{{}\begin{matrix}m^2=1\\2m^2< >1-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left\{1;-1\right\}\\2m^2+m-1< >0\end{matrix}\right.\)
=>m=1