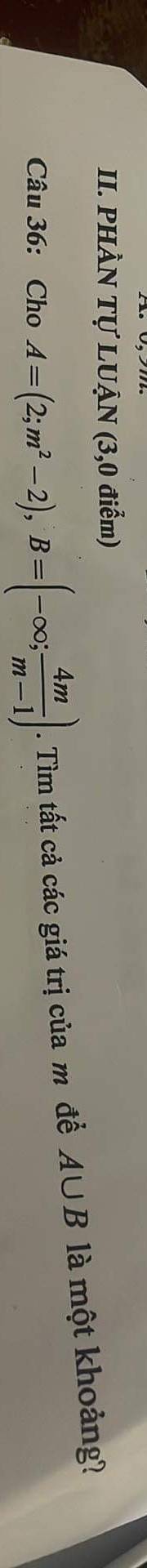Question

Answer 1

Để A hợp B là một khoảng thì 

\(\left\{{}\begin{matrix}2< m^2-2\\\dfrac{4m}{m-1}>=2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m^2-2>2\\\dfrac{4m-2\left(m-1\right)}{m-1}>=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m^2>4\\\dfrac{4m-2m+2}{m-1}>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\\\dfrac{m+1}{m-1}>=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\\\left[{}\begin{matrix}m>1\\m< =-1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -2\\m>2\end{matrix}\right.\)