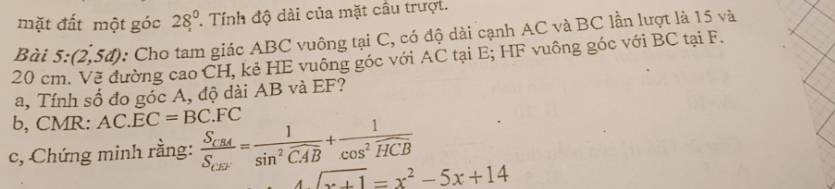a: ΔCBA vuông tại C
=>\(AB^2=CA^2+CB^2\)
=>\(AB^2=15^2+20^2=625\)
=>AB=25(cm)
Xét ΔABC vuông tại C có \(sinA=\dfrac{BC}{AB}=\dfrac{20}{25}=\dfrac{4}{5}\)
=>\(\widehat{A}\simeq53^0\)
XétΔABC vuông tại C có CH là đường cao
nên \(CH\cdot AB=CA\cdot CB\)
=>\(CH\cdot25=15\cdot20=300\)
=>CH=12(cm)
Xét tứ giác CEHF có
\(\widehat{CEH}=\widehat{CFH}=\widehat{FCE}=90^0\)
=>CEHF là hình chữ nhật
=>CH=EF=12(cm)
b: Xét ΔCHA vuông tại H có HE là đường cao
nên \(CE\cdot CA=CH^2\left(1\right)\)
Xét ΔCHB vuông tại H có HF là đường cao
nên \(CF\cdot CB=CH^2\left(2\right)\)
Từ (1) và (2) suy ra \(CE\cdot CA=CF\cdot CB\)