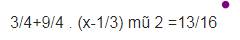\(\dfrac{3}{4}+\dfrac{9}{4}\left(x-\dfrac{1}{3}\right)^2=\dfrac{13}{16}\)
=>\(\dfrac{9}{4}\left(x-\dfrac{1}{3}\right)^2=\dfrac{13}{16}-\dfrac{3}{4}=\dfrac{1}{16}\)
=>\(\left(x-\dfrac{1}{3}\right)^2=\dfrac{1}{16}:\dfrac{9}{4}=\dfrac{1}{16}\cdot\dfrac{4}{9}=\dfrac{1}{36}\)
=>\(\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{1}{6}\\x-\dfrac{1}{3}=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{6}+\dfrac{1}{3}=\dfrac{1}{2}\\x=\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}\end{matrix}\right.\)
`3/4 + 9/4 (x-1/3)^2 =13/16`
`=> 9/4 (x-1/3)^2 =13/16-3/4`
`=> 9/4 (x-1/3)^2 =1/16`
`=> (x-1/3)^2 =1/16:9/4`
`=> (x-1/3)^2 =1/16 xx 4/9`
`=> (x-1/3)^2 =1/36`
`=> (x-1/3)^2 = (+- 1/6)^2`
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{1}{6}\\x-\dfrac{1}{3}=-\dfrac{1}{6}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{1}{6}\end{matrix}\right.\)