Question

Answer 1

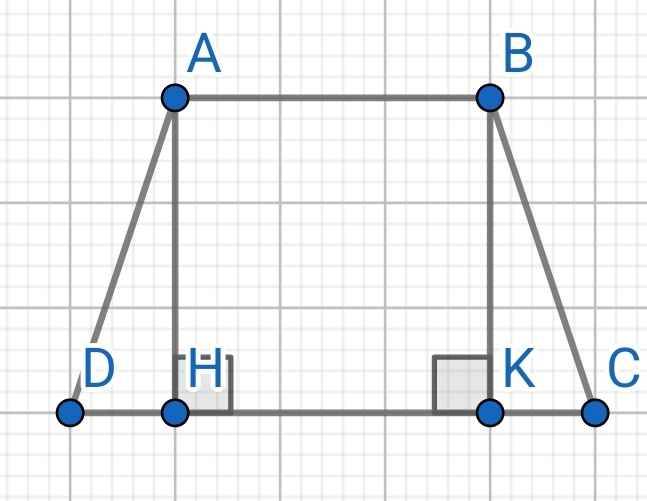
 a) Do ABCD là hình thang cân

⇒ AD = BC và ∠ADH = ∠BCK

Xét hai tam giác vuông: ∆AHD và ∆BKC có:

AD = BC (cmt)

∠ADH = ∠BCK (cmt)

⇒ ∆AHD = ∆BKC (cạnh huyền - góc nhọn)

b) Do AH ⊥ CD (gt)

BK ⊥ CD (gt)

⇒ AH // BK

Do ∆AHD = ∆BKC (cmt)

⇒ AH = BK (hai cạnh tương ứng)

Tứ giác ABKH có:

AH // BK (cmt)

AH = BK (cmt)

⇒ ABKH là hình bình hành

Mà ∠AHK = 90⁰ (gt)

⇒ ABKH là hình chữ nhật

⇒ AB = HK

c) Do ∆AHD = ∆BKC (cmt)

⇒ DH = CK (hai cạnh tương ứng)

Lại có AB = HK (cmt)

⇒ DC - AB = DC - HK

= DH + CK

Mà DH = CK (cmt)

⇒ DH + CK = 2CK

⇒ DC - AB = 2CK

⇒ CK = (DC - AB)/2