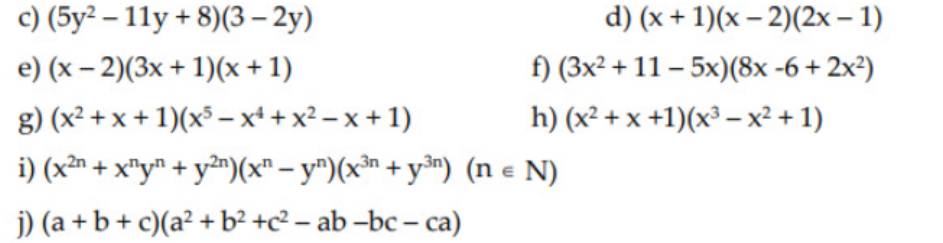c: \(\left(5y^2-11y+8\right)\left(-2y+3\right)\)
\(=-10y^3+15y^2+22y^2-33y-16y+24\)
\(=-10y^3+37y^2-47y+24\)
d: \(\left(x+1\right)\left(x-2\right)\left(2x-1\right)\)
\(=\left(x^2-x-2\right)\left(2x-1\right)\)
\(=2x^3-x^2-2x^2+x-4x+2\)
\(=2x^3-3x^2-3x+2\)
e: \(\left(x-2\right)\left(x+1\right)\left(3x+1\right)\)
\(=\left(x^2-x-2\right)\left(3x+1\right)\)
\(=3x^3+x^2-3x^2-x-6x-2\)
\(=3x^3-2x^2-7x-2\)
f: \(\left(3x^2-5x+11\right)\left(2x^2+8x-6\right)\)
\(=6x^4+24x^3-18x^2-10x^3-40x^2+30x+22x^2+88x-66\)
\(=6x^4+14x^3-36x^2+118x-66\)
i: \(=\left(x^{3n}-y^{3n}\right)\left(x^{3n}+y^{3n}\right)=x^{6n}-y^{6n}\)
j: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
Vậy: \(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=a^3+b^3+c^3-3abc\)