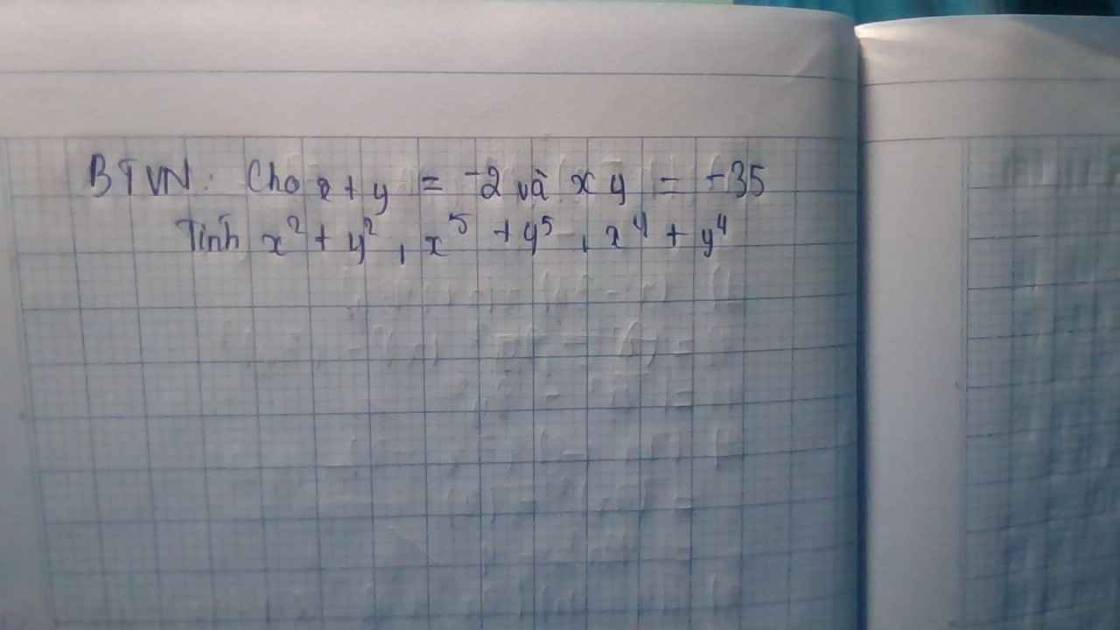\(x^2+y^2=\left(x+y\right)^2-2xy\)
\(=\left(-2\right)^2-2\cdot\left(-35\right)=74\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=74^2-2\left(xy\right)^2\)
\(=74^2-2\cdot\left(-35\right)^2=3026\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=\left(-2\right)^3-3\cdot\left(-2\right)\cdot\left(-35\right)=-218\)
\(x^5+y^5=\left(x^2+y^2\right)\left(x^3+y^3\right)-x^2y^3-x^3y^2\)
\(=74\cdot\left(-218\right)-x^2y^2\left(x+y\right)\)
\(=-16132-\left(-35\right)^2\cdot\left(-2\right)\)
\(=-13682\)
Đúng 0
Bình luận (0)
