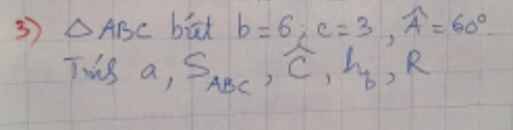Theo định lý côsin ta có:
\(a^2=b^2+c^2-2bc\cdot cosA\Rightarrow a=\sqrt{b^2+c^2-2bc\cdot cosA}\)
\(\Rightarrow a=\sqrt{6^2+3^2-2\cdot6\cdot3\cdot cos60^o}=3\sqrt{3}\)
\(p=\dfrac{a+b+c}{2}=\dfrac{6+3+3\sqrt{3}}{2}=\dfrac{9+3\sqrt{3}}{2}\)
Áp dụng công thức Heron ta có:
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(\Rightarrow S_{ABC}=\sqrt{\dfrac{9+3\sqrt{3}}{2}\cdot\left(\dfrac{9+3\sqrt{3}}{2}-3\sqrt{3}\right)\cdot\left(\dfrac{9+3\sqrt{3}}{2}-6\right)\cdot\left(\dfrac{9+3\sqrt{3}}{2}-3\right)}\) (1)
\(\Rightarrow S_{ABC}=\dfrac{9\sqrt{3}}{2}\)
Theo hệ quả của định lý côsin ta có:
\(cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{\left(3\sqrt{3}\right)^2+6^2-3^2}{2\cdot3\sqrt{3}\cdot6}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{C}=30^o\)
Theo công thức Heron ta có:
\(h_b=2\cdot\dfrac{\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\left(1\right)}{b}\)
\(\Rightarrow h_b=2\cdot\dfrac{\dfrac{9\sqrt{3}}{2}}{6}=\dfrac{3\sqrt{3}}{2}\) (theo kết quả (1))
Mà: \(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{3\sqrt{3}\cdot6\cdot3}{4\cdot\dfrac{9\sqrt{3}}{2}}=3\)