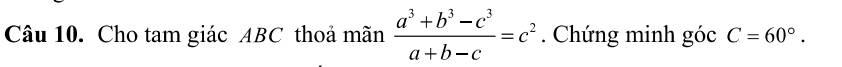\(\dfrac{a^3+b^3-c^3}{a+b-c}=c^2\)
=>\(\dfrac{\left(a+b\right)^3-c^3-3ba\left(a+b\right)}{a+b-c}=c^2\)
=>\(\dfrac{\left(a+b-c\right)\left[\left(a+b\right)^2+c\left(a+b\right)+c^2\right]-3ab\left(a+b\right)}{a+b-c}=c^2\)
=>\(\left(a+b\right)^2+c\left(a+b\right)+c^2-c^2-\dfrac{3ab\left(a+b\right)}{a+b-c}=0\)
=>\(\left(a+b\right)\left(a+b+c\right)-\dfrac{3ab\left(a+b\right)}{a+b-c}=0\)
=>\(\left(a+b\right)\left(a+b+c-\dfrac{3ab}{a+b-c}\right)=0\)
=>\(a+b+c-\dfrac{3ab}{a+b-c}=0\)
=>\(a+b+c=\dfrac{3ab}{a+b-c}\)
=>\(\left(a+b+c\right)\left(a+b-c\right)=3ab\)
=>\(\left(a+b\right)^2-c^2=3ab\)
=>\(a^2+b^2+2ab-c^2-3ab=0\)
=>\(c^2=a^2-ab+b^2\)(1)
Giả sử \(\widehat{C}=60^0\)
Xét ΔABC có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{b^2+a^2-c^2}{2\cdot b\cdot a}=cos60=\dfrac{1}{2}\)
=>\(b^2+a^2-c^2=ab\)
=>\(c^2=a^2+b^2-ab\)(2)
Từ (1),(2) suy ra \(\widehat{C}=60^0\) là đúng
=>\(\widehat{C}=60^0\)