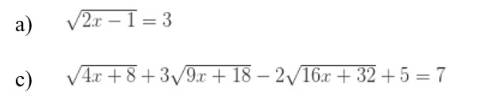\(a)\sqrt{2x-1}=3\\ \Leftrightarrow2x-1=9\\ \Leftrightarrow2x=10\\ \Leftrightarrow x=5\)
\(b)\sqrt{4x+8}+3\sqrt{9x+18}-2\sqrt{16x+32}+5=7\\ \Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-8\sqrt{x+2}+5=7\\ \Leftrightarrow\sqrt{x+2}\left(2+9-8\right)+5=7\\ \Leftrightarrow3\sqrt{x+2}+5=7\\ \Leftrightarrow3\sqrt{x+2}=2\\ \Leftrightarrow9x+18=4\\ \Leftrightarrow9x=-14\\ \Leftrightarrow x=-\dfrac{14}{9}\)
a) \(\sqrt[]{2x-1}=3\)
\(\Leftrightarrow2x-1=9\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\)
b) \(\sqrt[]{4x+8}+3\sqrt[]{9x+18}-2\sqrt[]{16x+32}+5=7\)
\(\Leftrightarrow\sqrt[]{4\left(x+2\right)}+3\sqrt[]{9\left(x+2\right)}-2\sqrt[]{16\left(x+2\right)}=2\)
\(\Leftrightarrow2\sqrt[]{x+2}+9\sqrt[]{x+2}-8\sqrt[]{x+2}=2\)
\(\Leftrightarrow3\sqrt[]{x+2}=2\)
\(\Leftrightarrow\sqrt[]{x+2}=\dfrac{2}{3}\)
\(\Leftrightarrow x+2=\dfrac{4}{9}\)
\(\Leftrightarrow x=\dfrac{4}{9}-2=-\dfrac{14}{4}=-\dfrac{7}{2}\)
a) ĐKXĐ: x ≥ 1/2
Phương trình đã cho tương đương:
2x - 1 = 9
⇔ 2x = 10
⇔ x = 5 (nhận)
Vậy S = {5}
c) √(4x + 8) + 3√(9x + 18) - 2√(16x + 32) + 5 = 7
⇔ 2√(x + 2) + 9√(x + 2) - 8√(x + 2) = 7 - 5
⇔ 3√(x + 2) = 2 (1)
ĐKXĐ: x ≥ -2
(1) ⇔ √(x + 2) = 2/3
⇔ x + 2 = 4/9
⇔ x = 4/9 - 2
⇔ x = -14/9 (nhận)
Vậy S = {-14/9}