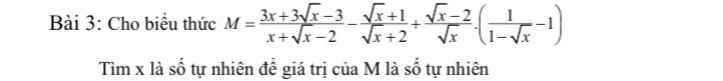\(M=\dfrac{3x+3\sqrt{x}-3-\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\left(\dfrac{-1}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{-1-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{2x+3\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-1-\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Để M là số tự nhiên thì \(\left\{{}\begin{matrix}M>=0\\\sqrt{x}-1+2⋮\sqrt{x}-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>1\\\sqrt{x}-1\in\left\{1;-1;2;-2\right\}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>1\\x\in\left\{4;9;0\right\}\end{matrix}\right.\)
=>x=4 hoặc x=9