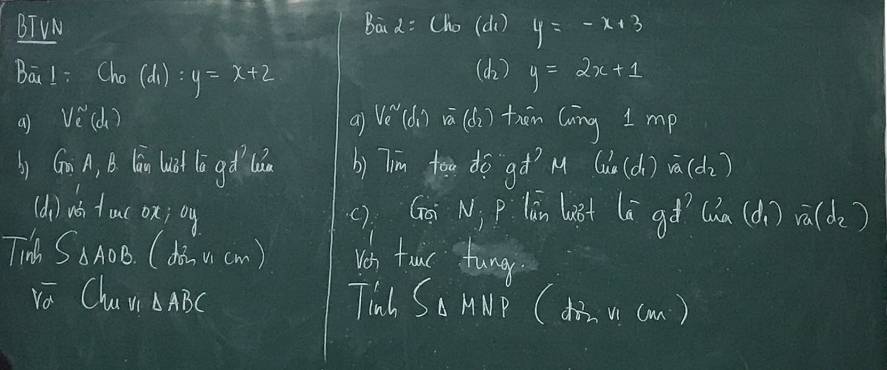2:
a: 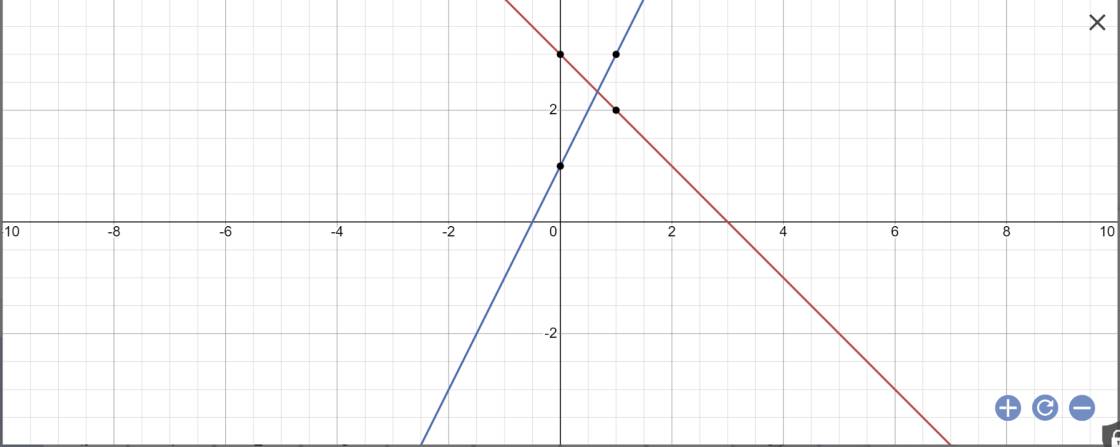
b: tọa độ M là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}2x+1=-x+3\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=2\\y=2x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=2\cdot\dfrac{2}{3}+1=\dfrac{4}{3}+1=\dfrac{7}{3}\end{matrix}\right.\)
c: Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+3=-0+3=3\end{matrix}\right.\)
Tọa độ P là:
\(\left\{{}\begin{matrix}x=0\\y=2x+1=2\cdot0+1=1\end{matrix}\right.\)
M(2/3;7/3); N(0;3); P(0;1)
\(MN=\sqrt{\left(0-\dfrac{2}{3}\right)^2+\left(3-\dfrac{7}{3}\right)^2}=\dfrac{2\sqrt{2}}{3}\)
\(MP=\sqrt{\left(0-\dfrac{2}{3}\right)^2+\left(1-\dfrac{7}{3}\right)^2}=\dfrac{2\sqrt{5}}{3}\)
\(NP=\sqrt{\left(0-0\right)^2+\left(1-3\right)^2}=2\)
Xét ΔMNP có \(cosM=\dfrac{MN^2+MP^2-NP^2}{2\cdot MN\cdot MP}=\dfrac{-1}{\sqrt{10}}\)
=>\(sinM=\dfrac{3}{\sqrt{10}}\)
\(S_{MNP}=\dfrac{1}{2}\cdot MN\cdot MP\cdot sinM=\dfrac{1}{2}\cdot\dfrac{2\sqrt{2}}{3}\cdot\dfrac{2\sqrt{5}}{3}\cdot\dfrac{3}{\sqrt{10}}\)
\(=\dfrac{1}{2}\cdot\dfrac{4}{9}\cdot3=\dfrac{2}{9}\cdot3=\dfrac{2}{3}\)