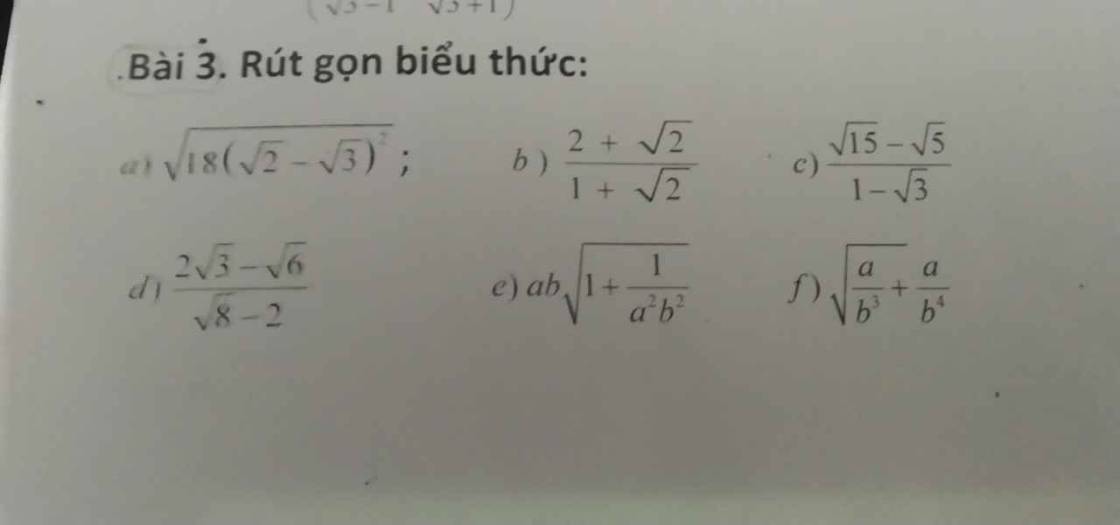a) \(\sqrt{18\left(\sqrt{2}-\sqrt{3}\right)^2}\)
\(=\sqrt{18}\left|\sqrt{2}-\sqrt{3}\right|\)
\(=-3\sqrt{2}\left(\sqrt{2}-\sqrt{3}\right)\)
\(=-3\cdot2+3\sqrt{2}\cdot\sqrt{3}\)
\(=3\sqrt{6}-6\)
b) \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}\)
\(=\sqrt{2}\)
c) \(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\)
\(=-\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(=-\sqrt{5}\)
\(a,\sqrt{18\left(\sqrt{2}-\sqrt{3}\right)^2}=\sqrt{18}.\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}\\ =\sqrt{3^2.2}.\left|\sqrt{2}-\sqrt{3}\right|=3\sqrt{2}\left(\sqrt{3}-\sqrt{2}\right)=3\sqrt{6}-6\\ b,\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(1-\sqrt{2}\right)}{\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)}=\dfrac{2+\sqrt{2}-2\sqrt{2}-2}{1-\left(\sqrt{2}\right)^2}\\ =\dfrac{-\sqrt{2}}{1-2}=\dfrac{-\sqrt{2}}{-1}=\sqrt{2}\)
d) \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}\)
\(=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\sqrt{2}-2}\)
\(=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}\)
\(=\dfrac{\sqrt{6}}{2}\)
e) \(ab\sqrt{1+\dfrac{1}{a^2b^2}}\)
\(=ab\sqrt{\dfrac{a^2b^2+1}{a^2b^2}}\)
\(=\sqrt{a^2b^2\cdot\dfrac{a^2b^2+1}{a^2b^2}}\)
\(=\sqrt{a^2b^2+1}\)
f) \(\sqrt{\dfrac{a}{b^3}}+\dfrac{a}{b^4}\)
\(=\dfrac{\sqrt{a}}{b\sqrt{b}}+\dfrac{a}{b^4}\)
\(=\dfrac{b^3\sqrt{a}}{b^4\sqrt{b}}+\dfrac{a\sqrt{b}}{b^4\sqrt{b}}\)
\(=\dfrac{b^3\sqrt{a}+a\sqrt{b}}{b^4\sqrt{b}}\)
\(=\dfrac{\sqrt{b}\left(b^2\sqrt{ab}+a\right)}{b^4\sqrt{b}}\)
\(=\dfrac{b^2\sqrt{ab}+a}{b^4}\)