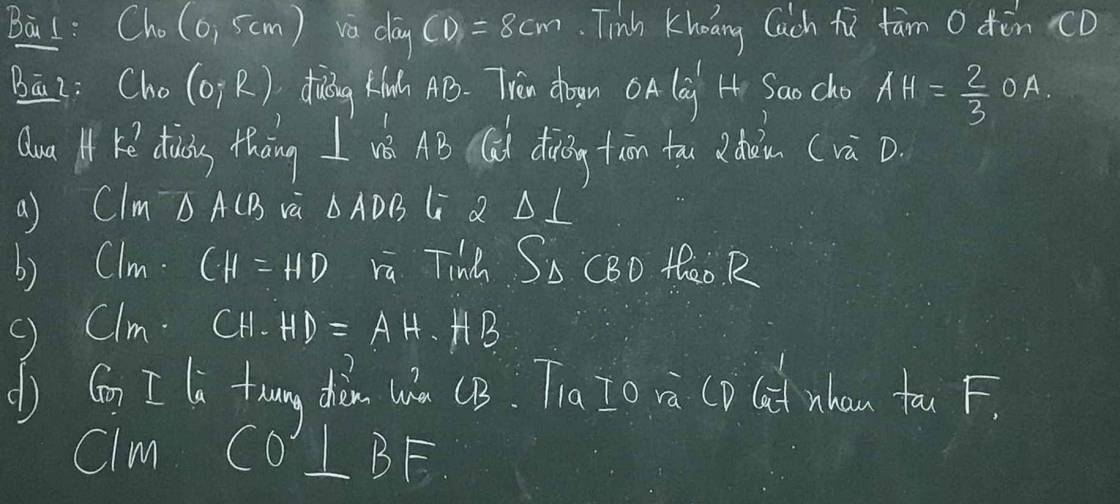2:
a: Xét (O) có
góc ACB, góc ADB là hai góc nội tiếp chắn nửa đường tròn
=>góc ACB=góc ADB=90 độ
=>ΔACB vuông tại C, ΔADB vuông tại D
b: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
=>HC=HD
AH=2/3AO
=>AH=2/3R
BH=2R-2/3R=4/3R
AH=2/3R
=>OH=1/3R
\(CH=\sqrt{R^2-\left(\dfrac{1}{3}R\right)^2}=R\cdot\dfrac{2\sqrt{2}}{3}\)
=>\(CD=R\cdot\dfrac{4\sqrt{2}}{3}\)
\(S_{CBD}=\dfrac{1}{2}\cdot BH\cdot CD\)
\(=\dfrac{1}{2}\cdot R\cdot\dfrac{4\sqrt{2}}{3}\cdot\dfrac{4}{3}R=\dfrac{8\sqrt{2}}{9}R^2\)
c: Xét ΔCAB vuông tại C có CH là đường cao
nên AH*HB=CH^2
=>AH*HB=CH*HD
Đúng 1
Bình luận (0)
