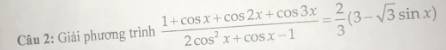ĐKXĐ: x<>pi+k2pi và x<>pi/3+k2pi và x<>-pi/3+k2pi
PT\(\Leftrightarrow\dfrac{1+cos2x+cos3x+cosx}{2cos^2x+2cosx-cosx-1}=2-\dfrac{2\sqrt{3}}{3}\cdot sinx\)
=>\(\dfrac{2cos^2x+2\cdot cos2x\cdot cosx}{\left(cosx+1\right)\left(2cosx-1\right)}=2-\dfrac{2\sqrt{3}}{3}\cdot sinx\)
=>\(\dfrac{2\cdot cosx\left(cosx+cos2x\right)}{2cos^2x+cosx-1}=2-\dfrac{2\sqrt{3}}{3}\cdot sinx\)
=>\(\dfrac{2\cdot cosx\left(2cos^2x-1+cosx\right)}{2cos^2x+cosx-1}=2-\dfrac{2\sqrt{3}}{3}\cdot sinx\)
=>\(2\cdot cosx=2-\dfrac{2\sqrt{3}}{3}\cdot sinx\)
=>\(cosx=1-\dfrac{\sqrt{3}}{3}\cdot sinx\)
\(\Leftrightarrow sinx\cdot\dfrac{\sqrt{3}}{3}+cosx=1\)
=>\(sinx\cdot\dfrac{\sqrt{3}}{3}:\sqrt{\dfrac{1}{3}+1}+cosx:\sqrt{\dfrac{1}{3}+1}=1:\sqrt{\dfrac{1}{3}+1}\)
=>\(sinx\cdot\dfrac{1}{2}+cosx\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\)
=>sin(x+pi/3)=căn 3/2
=>x+pi/3=pi/3+k2pi hoặc x+pi/3=2/3pi+k2pi
=>x=k2pi hoặc x=pi/3+k2pi(loại)