`A = 1/(1xx2) + 1/(2xx3) + ... + 1/(2023 xx2024)`
`A = 1 - 1/2 + 1/2 - 1/3 + ... + 1/2023 - 1/2024`
`A = 1- 1/2024`
`A = 2023/2024`
`B = 2/(1xx3) + 2/(3xx5) + ... + 2/(101xx103)`
`B = 1 - 1/3 + 1/3 - 1/5 + ... + 1/101 - 1/103`
`B = 1 - 1/103`
`B = 102/103`
`C = 1/(1xx4) + 1/(4xx7) + ... + 1/(304xx307)`
`3C = 3/(1xx4) + 3/(4xx7) + ... + 3/(304xx307)`
`3C = 1 - 1/4 + 1/4 - 1/7 + ... +1/304 - 1/307`
`3C = 306/307`
`C = 102/307`
a, \(A=\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{2023\times2024}\\ A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\\ A=1-\dfrac{1}{2024}=\dfrac{2023}{2024}\)
b, \(B=\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+...+\dfrac{2}{101\times103}\\ B=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{101}-\dfrac{1}{103}\\ B=1-\dfrac{1}{103}\\ B=\dfrac{102}{103}\)
c, \(3C=\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+...+\dfrac{3}{304\times307}\\ 3C=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{304}-\dfrac{1}{307}\\ C=\dfrac{1}{3}\left(1-\dfrac{1}{307}\right)\\ C=\dfrac{102}{307}\)
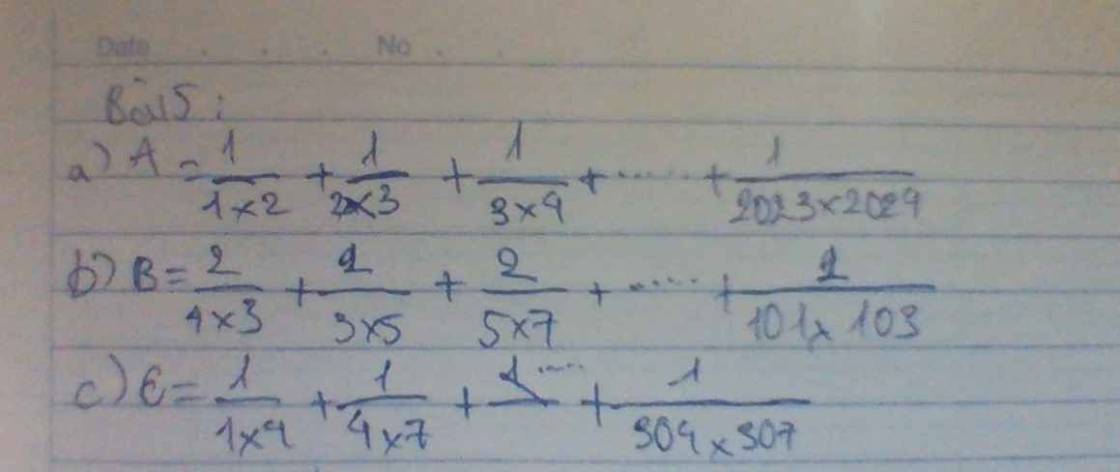


 4 và 5
4 và 5