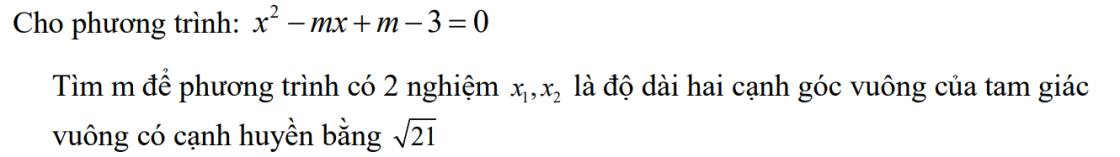\(x^2-mx+m-3=0\)
Để pt có 2 nghiệm \(x_1,x_2\) thì \(\Delta>0\Leftrightarrow\left(-m\right)^2-4m+12>0\) \(\Rightarrow\Delta\) vô nghiệm
Theo Vi ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=m-3\end{matrix}\right.\)
Vì 2 nghiệm \(x_1,x_2\left(x_1,x_2>0\right)\) là độ dài hai cạnh góc vuông của \(\Delta\) vuông có cạnh huyền bằng \(\sqrt{21}\) nên ta có :
\(x_1^2+x_2^2=\sqrt{21}^2\) \(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=21\)
\(\Leftrightarrow m^2-2\left(m-3\right)=21\)
\(\Leftrightarrow m^2-2m+6-21=0\)
\(\Leftrightarrow m^2-2m-15=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=5\\m=-3\end{matrix}\right.\)
Vậy \(m=5,m=-3\) thỏa mãn đề bài.
x1^2+x2^2=21
=>(x1+x2)^2-2x1x2=21
=>m^2-2m+6-21=0
=>(m-5)(m+3)=0
=>m=5 hoặc m=-3