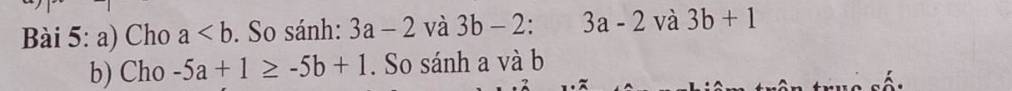Question

Answer 1

Lời giải:
a.

$3a-2-(3b-2)=3(a-b)<0$ do $a<b$

$\Rightarrow 3a-2< 3b-2$

$3a-2< 3b-2$

Mà $3b-2< 3b+1$

$\Rightarrow 3a-2< 3b+1$

b.

$-5a+1\geq -5b+1$

$\Rightarrow -5a+1-(-5b+1)\geq 0$

$\Rightarrow 5(b-a)\geq 0$

$\Rightarrow b-a\geq 0\Rightarrow b\geq a$

Answer 2

a) *) \(a< b\)

\(\Rightarrow3a< 3b\) (Nhân hai vế của bất đẳng thức với 3 > 0)

\(\Rightarrow3a-2< 3b-2\) (cộng hai vế với -2)  (1)

*) Ta có:

\(-2< 1\)

\(\Rightarrow3b-2< 3b+1\) (cộng hai vế với 3b)   (2)

Từ (1) và (2) \(\Rightarrow3a-2< 3b+1\)

b) \(-5a+1\ge-5b+1\)

\(\Rightarrow-5a\ge-5b\)  (cộng hai vế của hai vế với \(-1\))

\(\Rightarrow a\le b\) (chia cả hai vế của bất đẳng thức với -5 < 0)