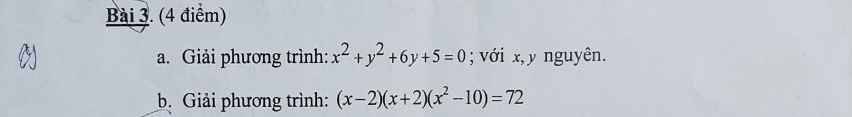a) \(x^2+y^2+6y+5=0\)
\(\Leftrightarrow x^2+\left(y+3\right)^2=4\left(1\right)\)
\(\Rightarrow x^2\le4\Rightarrow-2\le x\le2\)
Vì x là số nguyên nên \(x\in\left\{-2;-1;0;1;2\right\}\)
*Với \(x=\pm2\). \(\left(1\right)\Rightarrow\left(y+3\right)^2=0\Leftrightarrow y=-3\)
*Với \(x=\pm1\Rightarrow\left(y+3\right)^2=3\) (loại)
*Với \(x=0\Rightarrow\left(y+3\right)^2=4\Leftrightarrow\left[{}\begin{matrix}y+3=2\\y+3=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=-1\\y=-5\end{matrix}\right.\)
Vậy các nghiệm nguyên (x;y) của phương trình đã cho là \(\left(2;-3\right),\left(-2;-3\right),\left(0;-1\right),\left(0;-5\right)\)
b: =>(x^2-4)(x^2-10)=72
=>x^4-14x^2+40-72=0
=>x^4-14x^2-32=0
=>(x^2-16)(x^2+2)=0
=>x^2-16=0
=>x=4; x=-4