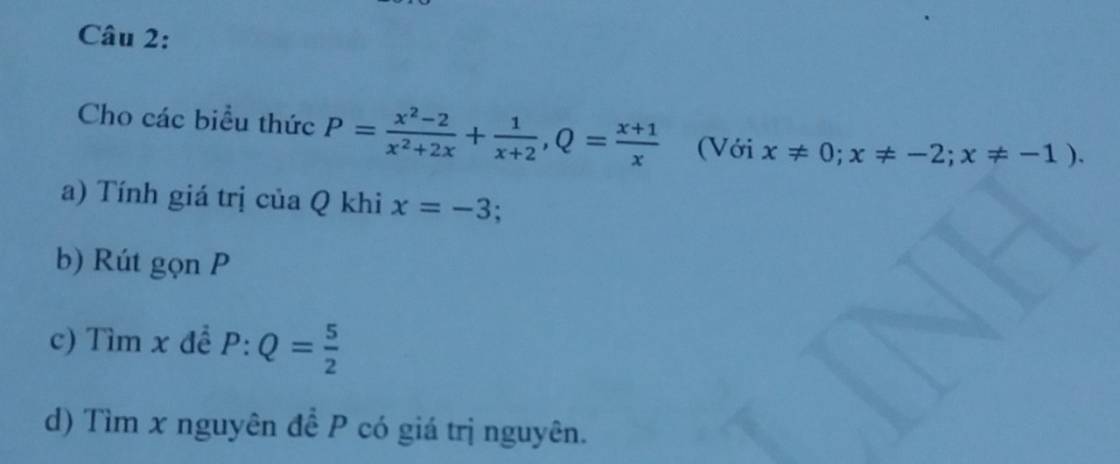\(a,\) Thay \(x=-3\) vào \(Q=\dfrac{x+1}{x}\) \(\left(x\ne0\right)\)
\(\Rightarrow Q=\dfrac{-3+1}{-3}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
\(b,P=\dfrac{x^2-2}{x^2+2x}+\dfrac{1}{x+2}\left(x\ne0,x\ne-2,x\ne-1\right)\)
\(=\dfrac{x^2-2}{x\left(x+2\right)}+\dfrac{1}{x+2}\)
\(=\dfrac{x^2-1+x}{x\left(x+2\right)}\)
\(=\dfrac{x^2+x-1}{x^2+2x}\)
\(c,P:Q=\dfrac{5}{2}\Leftrightarrow\dfrac{x^2+x-1}{x^2+2x}:\dfrac{x+1}{x}=\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{x^2+x-1}{x\left(x+2\right)}.\dfrac{x}{x+1}=\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{x^2+x-1}{\left(x+2\right)\left(x+1\right)}-\dfrac{5}{2}=0\)
\(\Leftrightarrow\dfrac{x^2+x-1}{x^2+3x+2}-\dfrac{5}{2}=0\)
\(\Leftrightarrow2\left(x^2+x-1\right)-5\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow2x^2+2x-2-5x^2-15x-10=0\)
\(\Leftrightarrow-3x^2-13x-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{3}\\x=-3\end{matrix}\right.\)