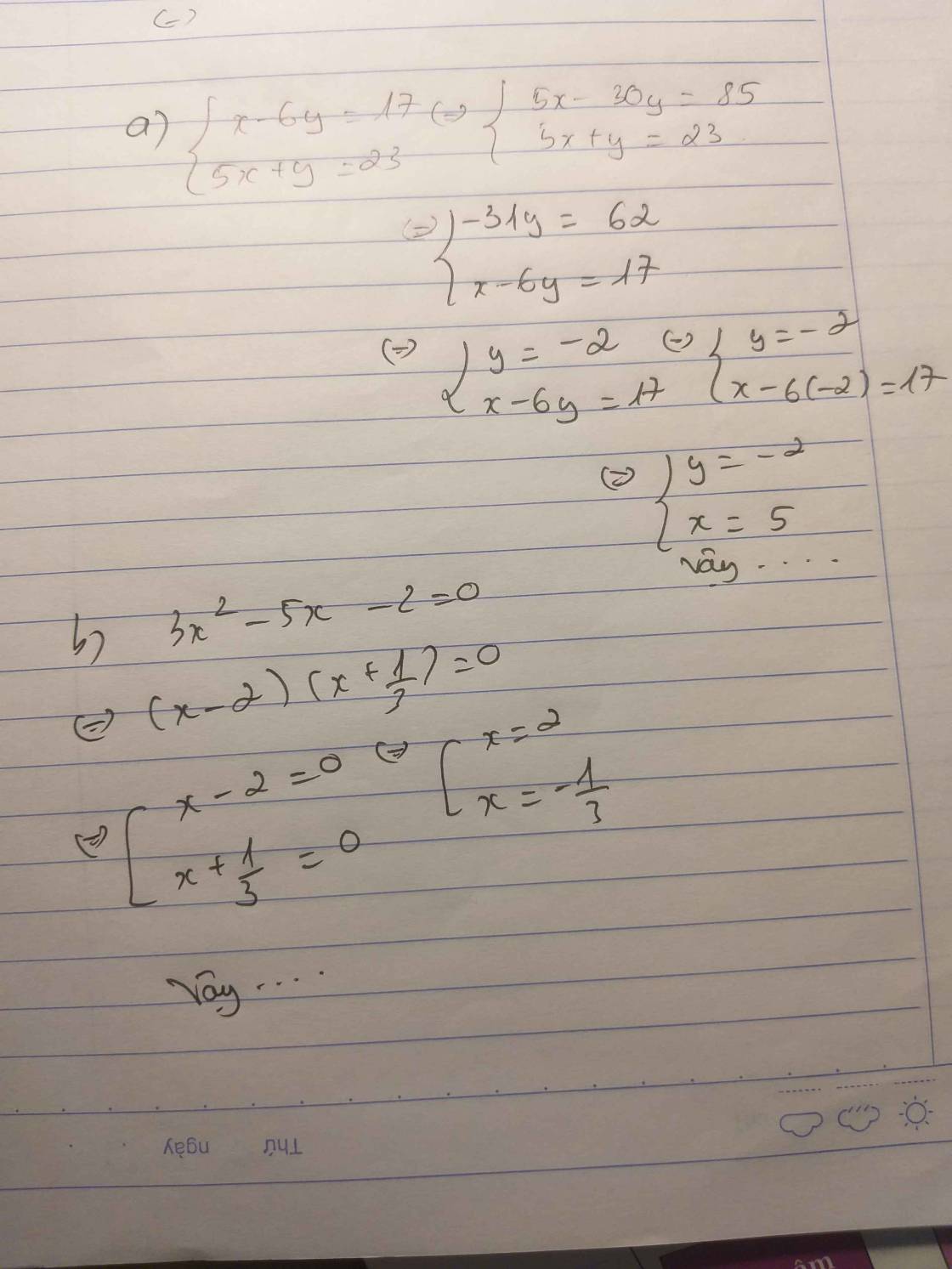1a/
\(\left\{{}\begin{matrix}x-6y=17\\5x+y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=17+6y\\5.\left(17+6y\right)+y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=17+6y\\85+30y+y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=17+6y\\31y=-62\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=17+6y\\y=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=17+6.\left(-2\right)\\y=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-2\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm là (x;y)=(5;-2)
1b/
3x2-5x-2=0
\(\Delta=\left(-5\right)^2-4.3.\left(-2\right)=25+24=49>0\) => Phương trình có 2 nghiệm phân biệt
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-\left(-5\right)-\sqrt{49}}{2.3}=-\dfrac{1}{3}\\x_2=\dfrac{-\left(-5\right)+\sqrt{49}}{2.3}=2\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là S={-1/3;2}
2:
a: Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: PTHĐGĐ là:
3x^2-4x+1=0
=>(x-1)(3x-1)=0
=>x=1/3 hoặc x=1
=>y=3 hoặc y=3*1/9=1/3