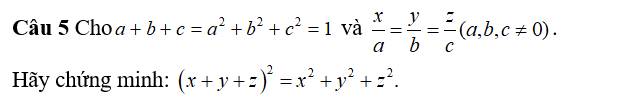Question

Answer 1

Đặt `x/a=y/b=z/c=k`

\(\Rightarrow\left\{{}\begin{matrix}x=ak\\y=bk\\z=ck\end{matrix}\right.\)

Với `x=ak;y=bk;z=ck` , ta đc :

`(x+y+z)^2=(ak+bk+ck)^2=[k*(a+b+c)]^2=(k*1)^2=k^2` ( do `a+b+c=1` ) (1)

\(x^2+y^2+z^2=\left(ak\right)^2+\left(bk\right)^2+\left(ck\right)^2=a^2\cdot k^2+b^2\cdot k^2+c^2\cdot k^2\\ =k^2\cdot\left(a^2+b^2+c^2\right)=k^2\cdot1=k^2\)(do `a^2+b^2+c^2=1` ) (2)

Từ (1) và (2) suy ra \(\left(x+y+z\right)^2=x^2+y^2+z^2\)